Abstract

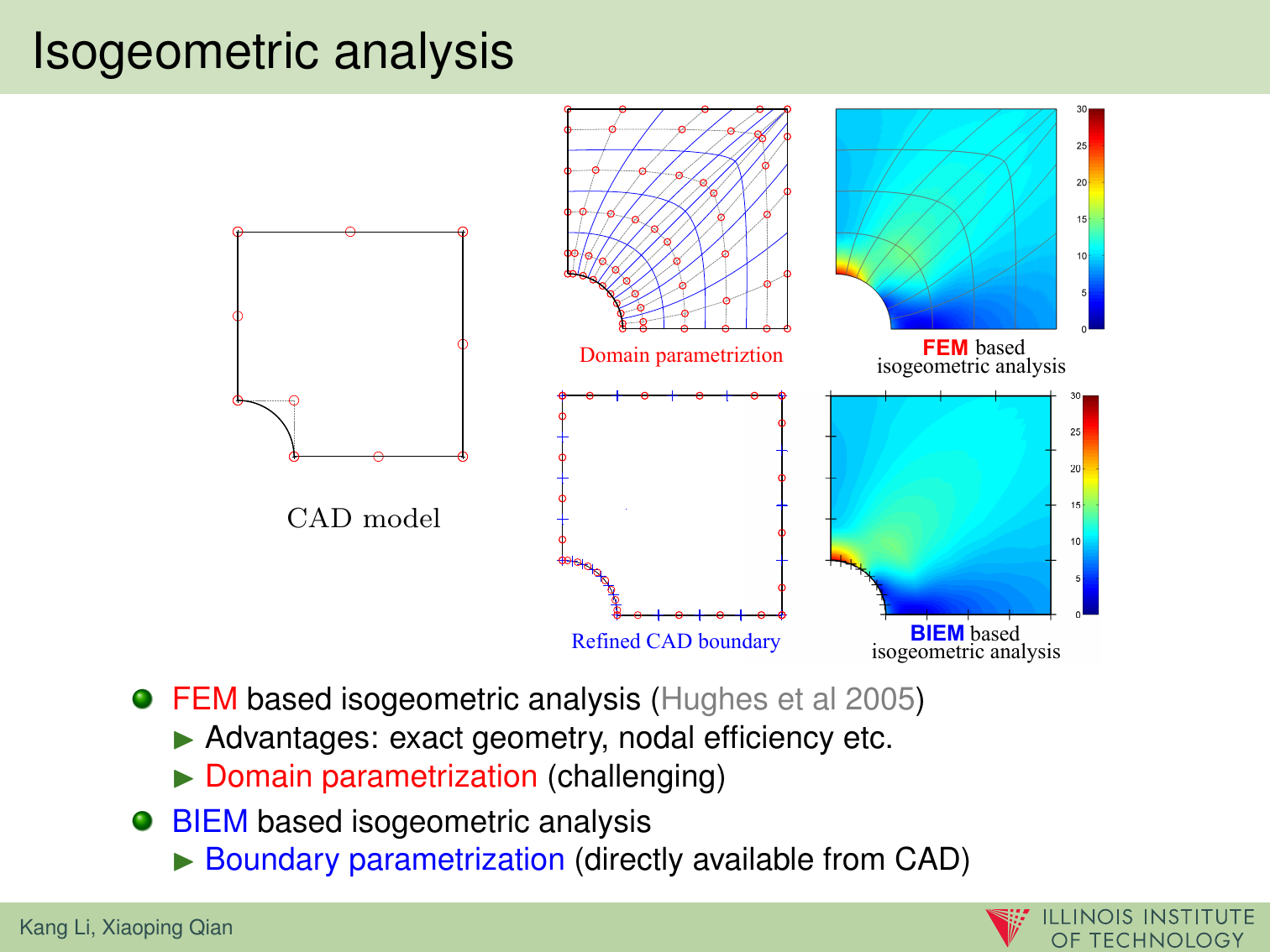
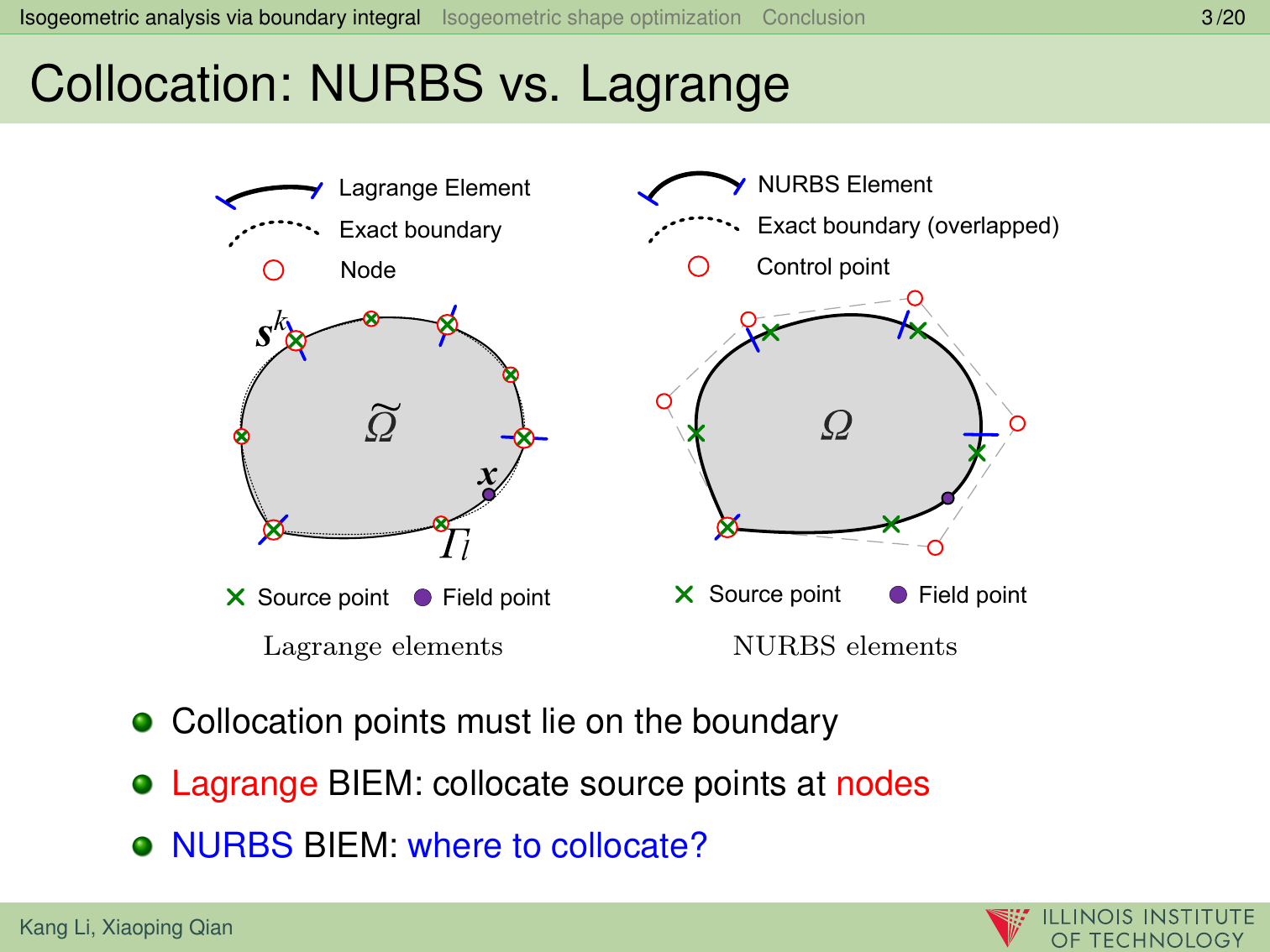
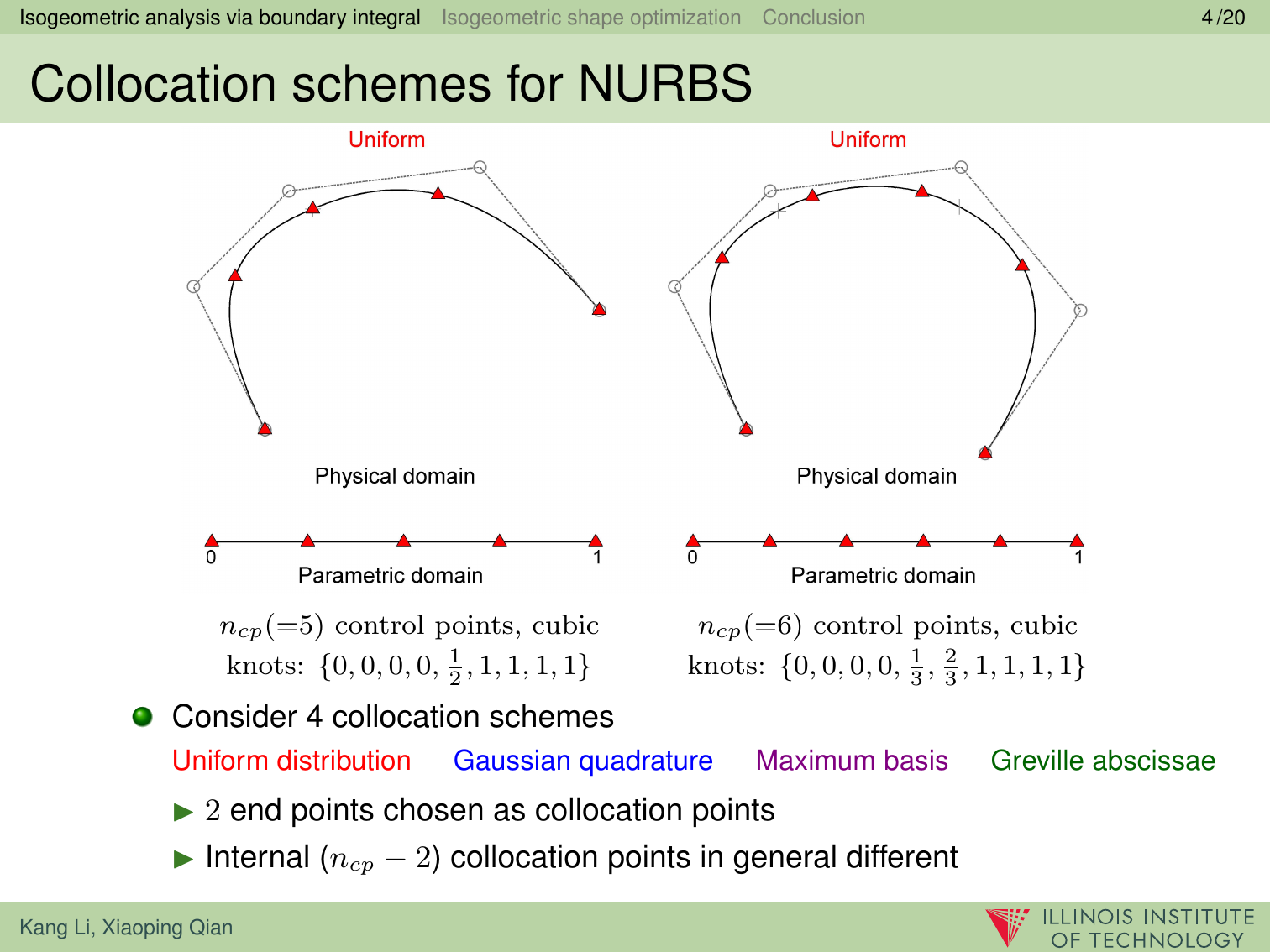
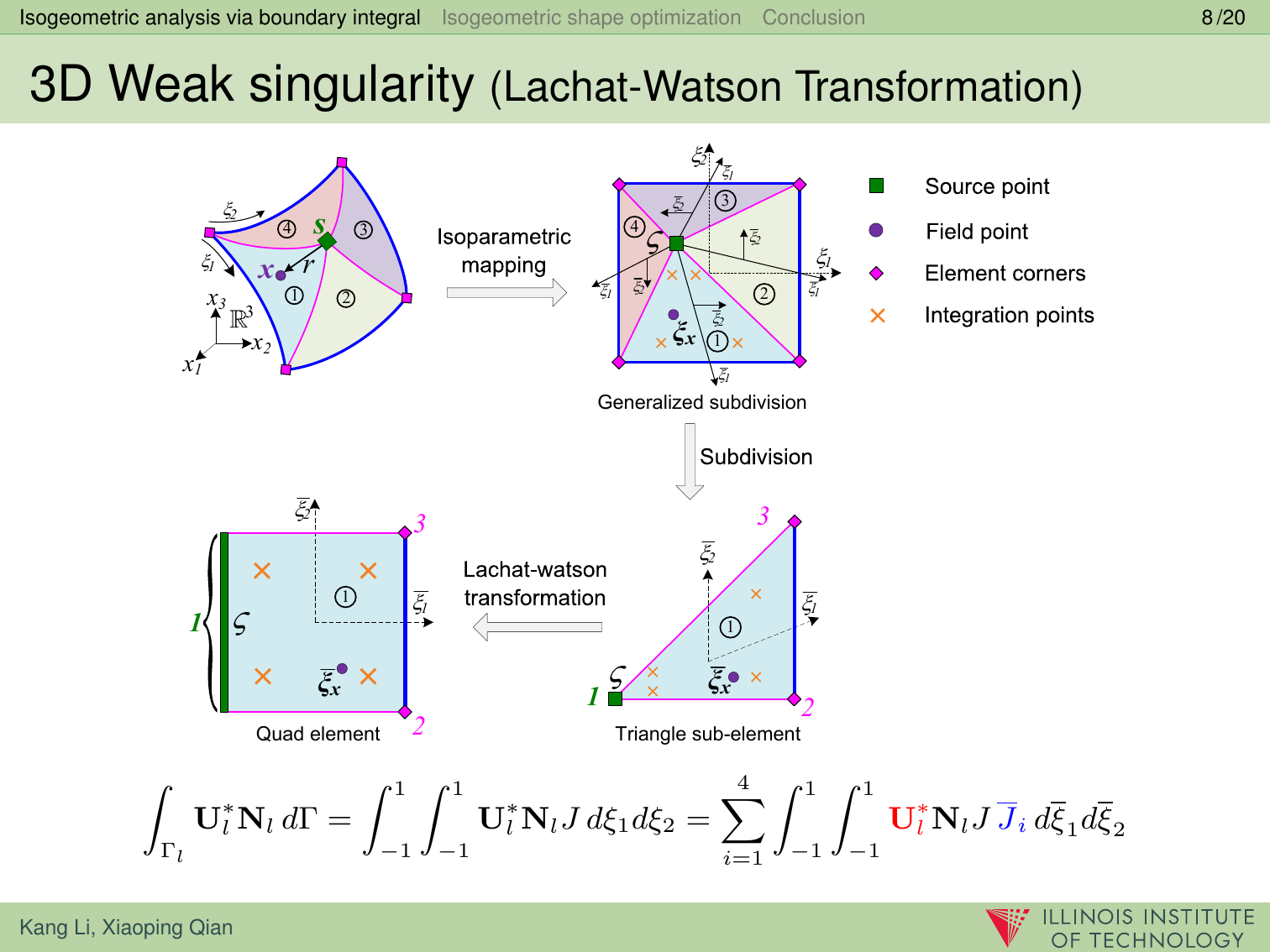
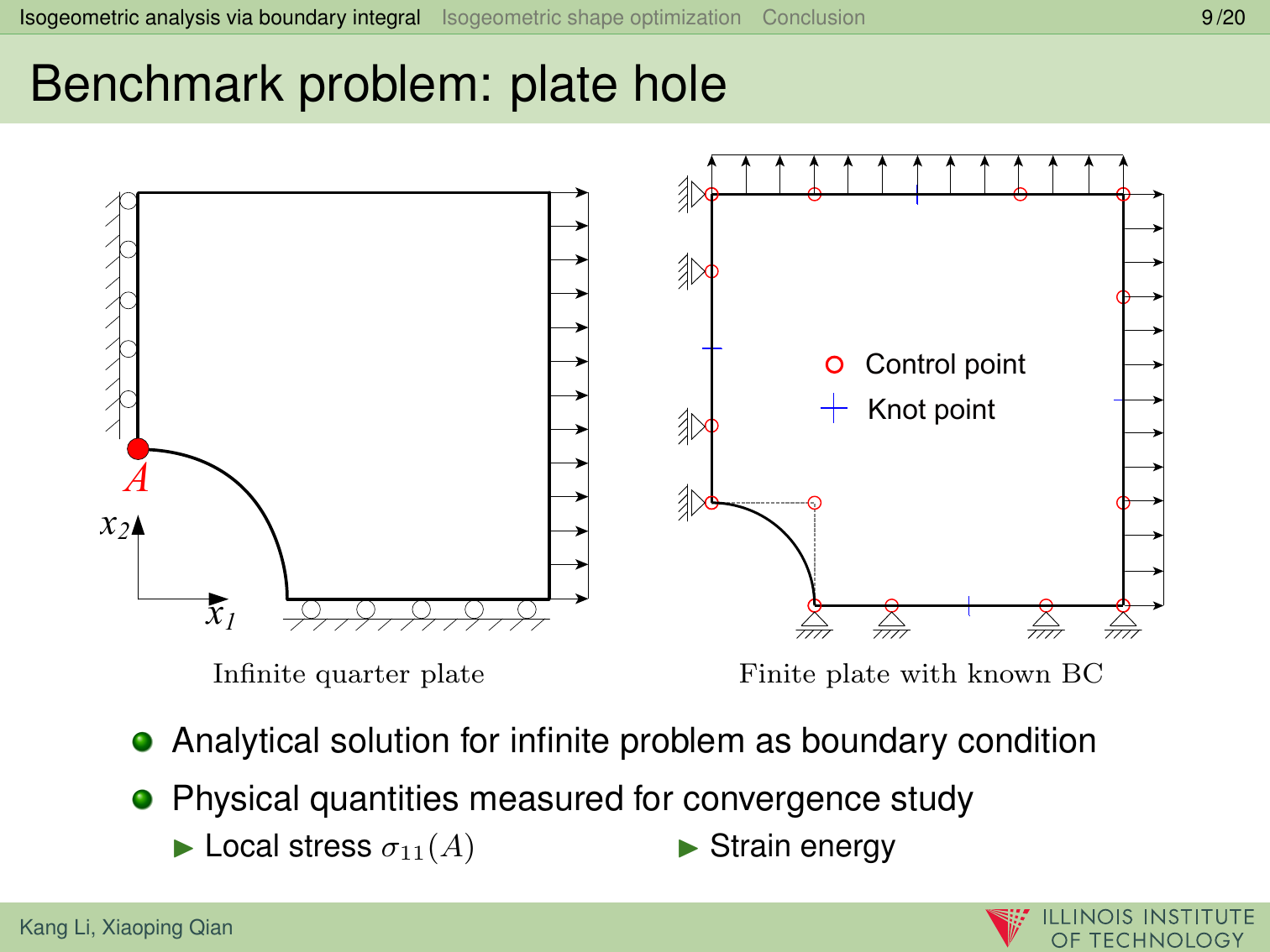
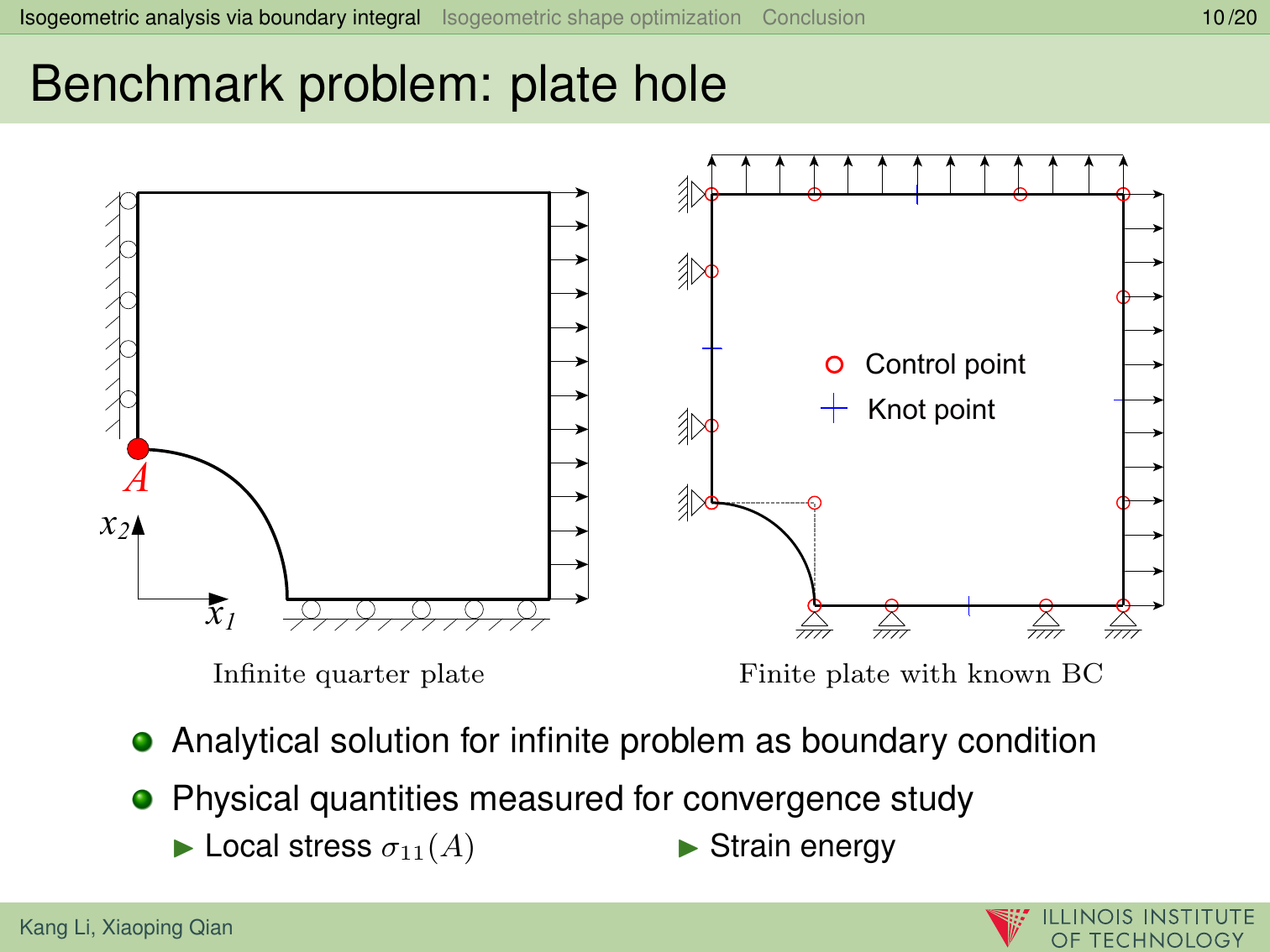
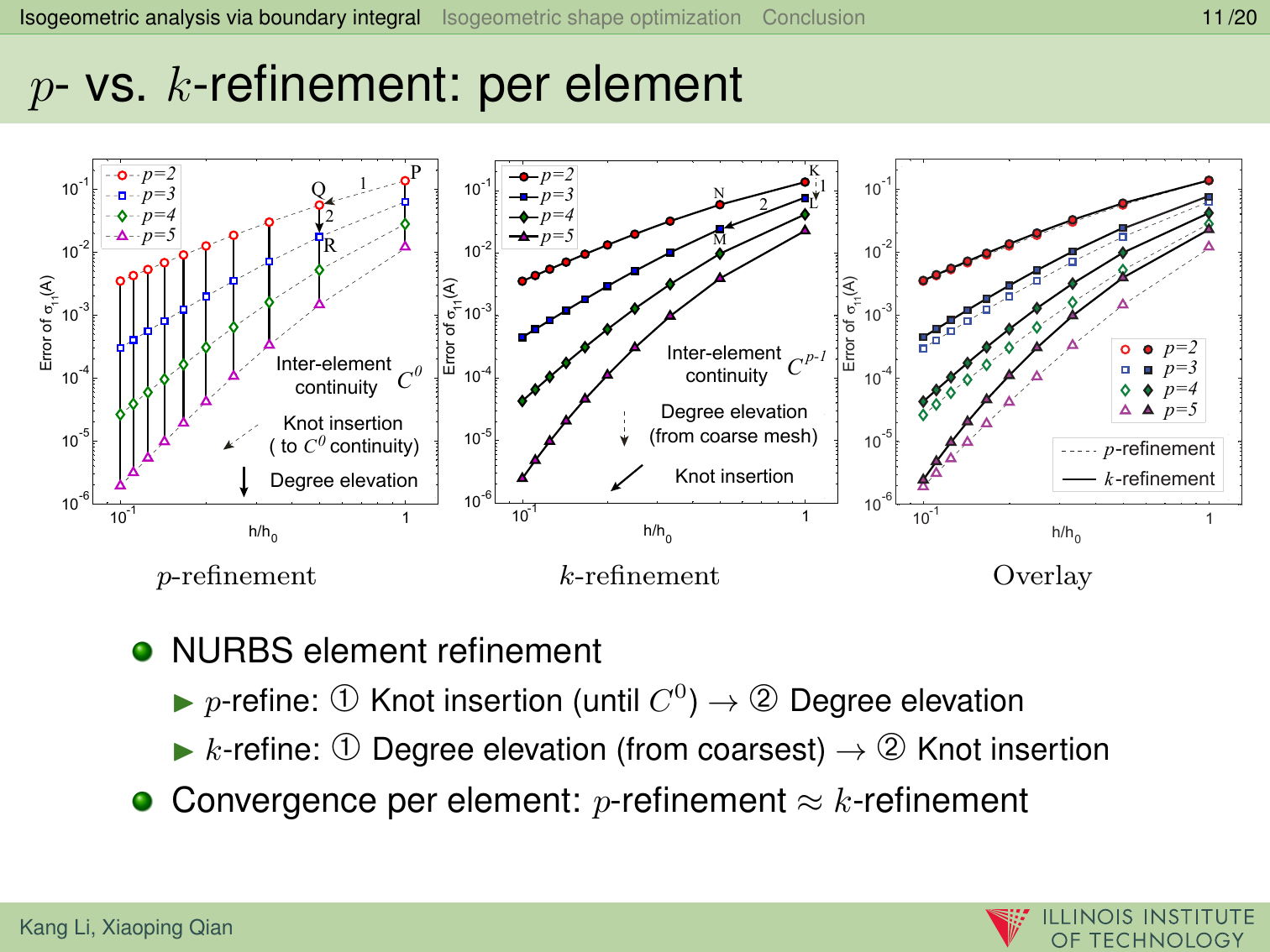
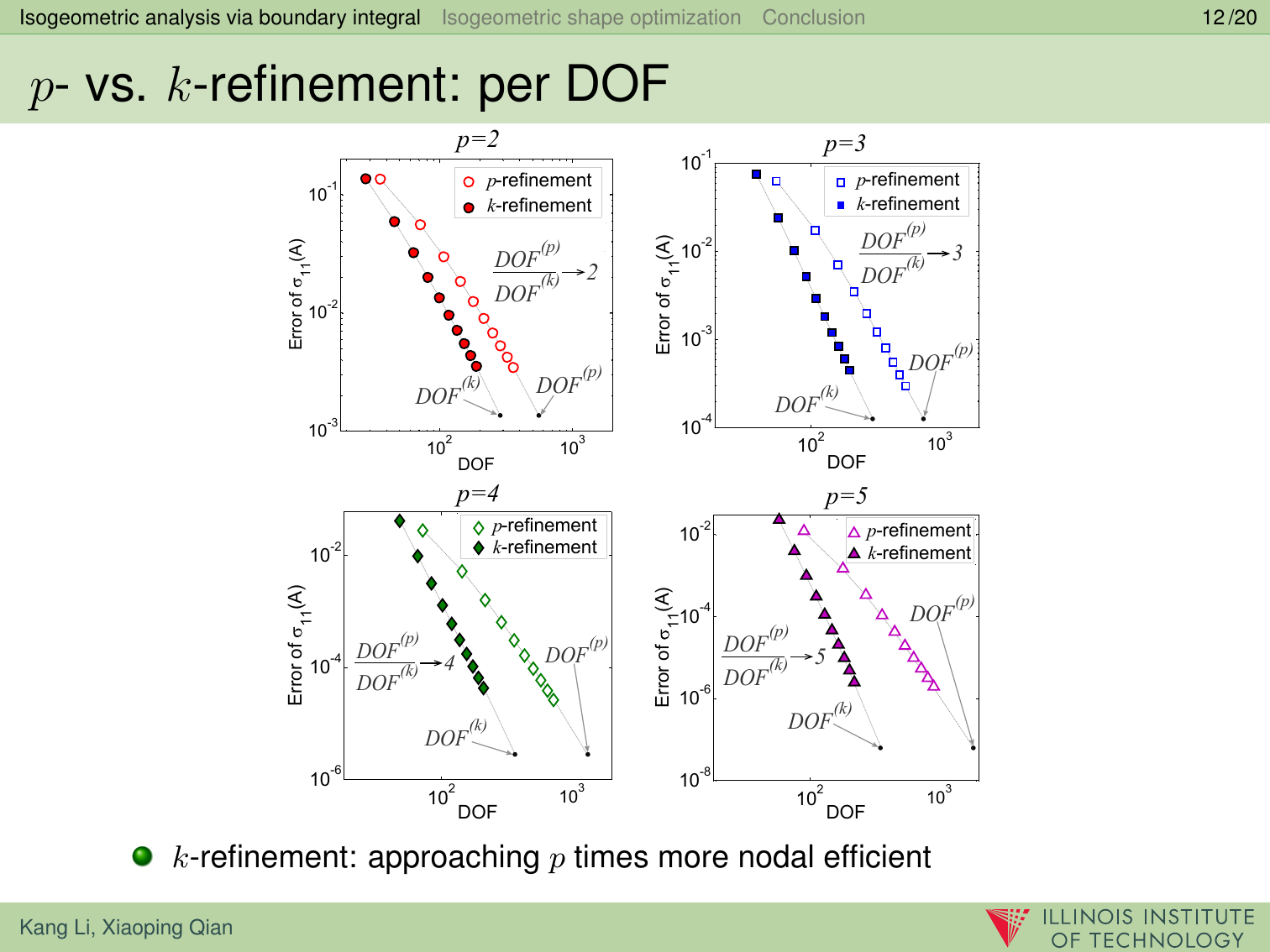
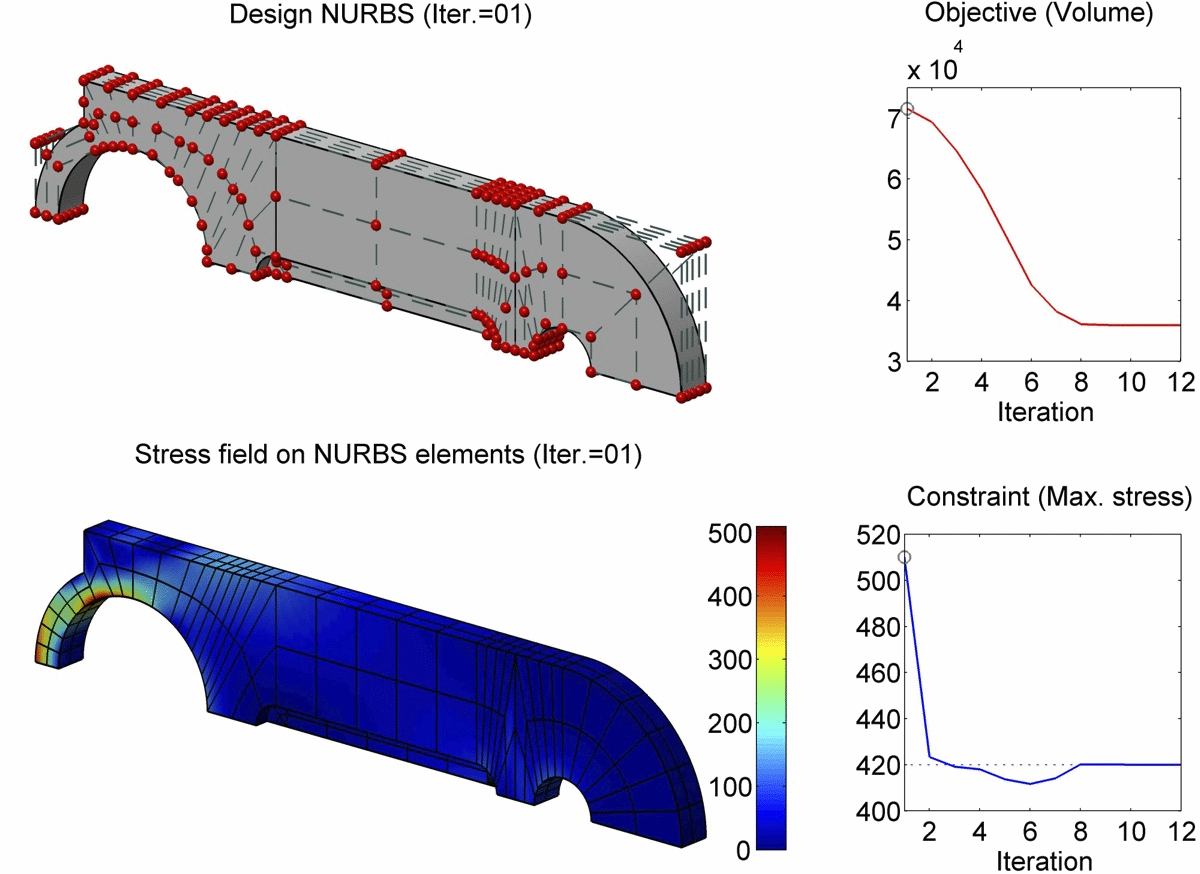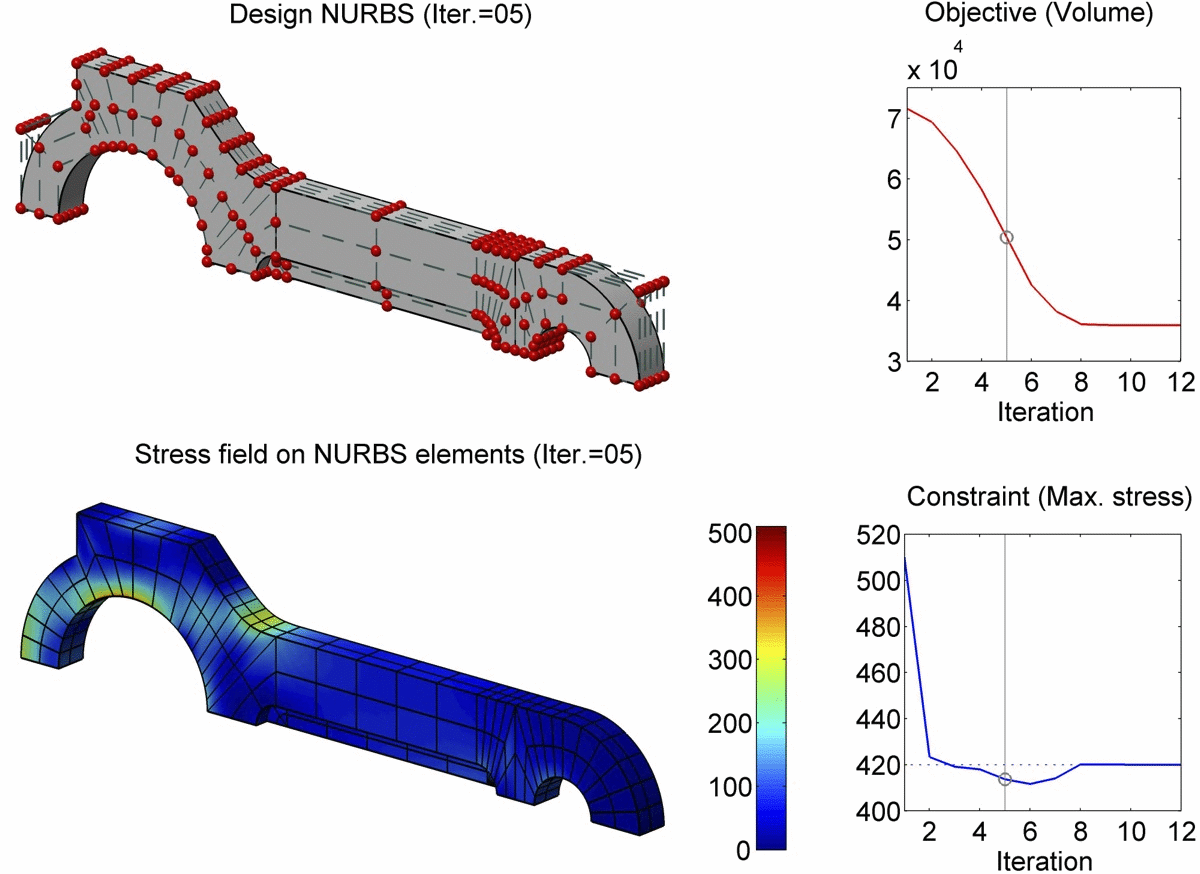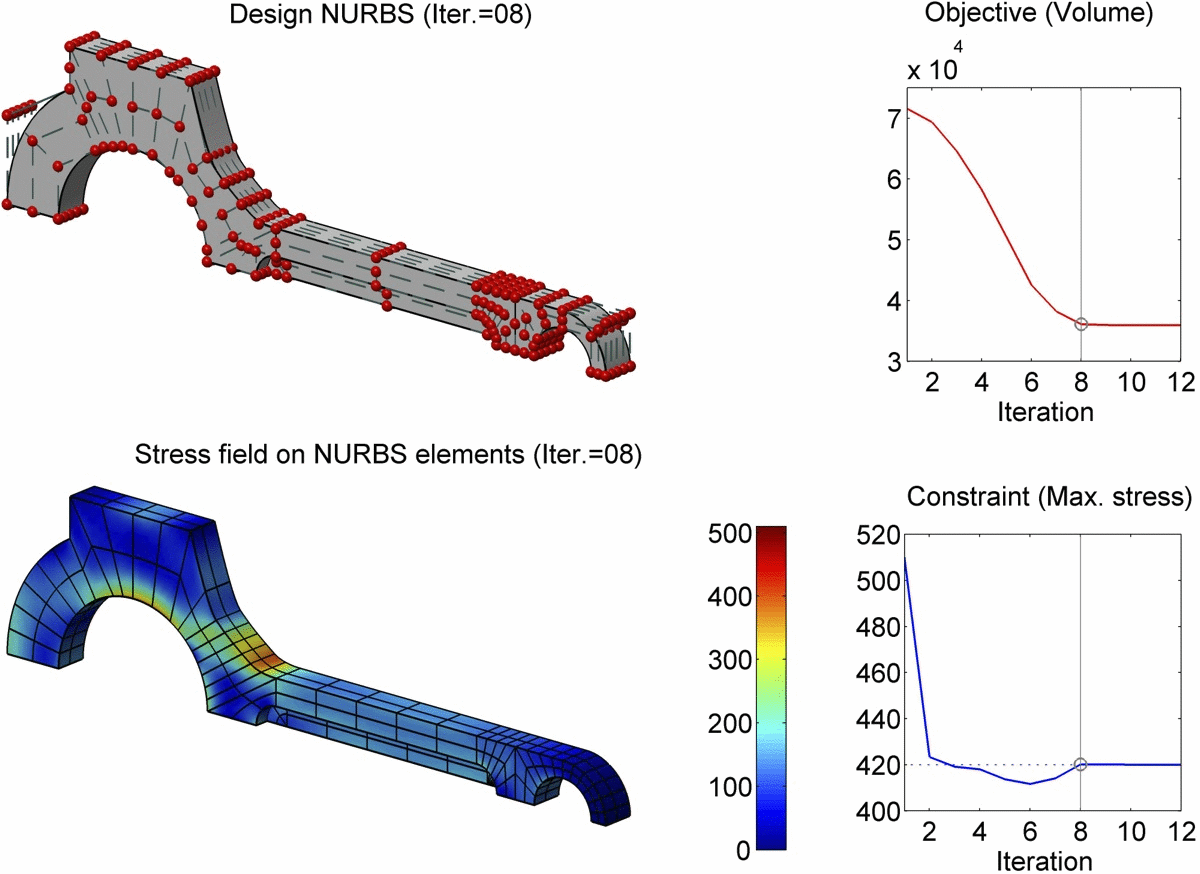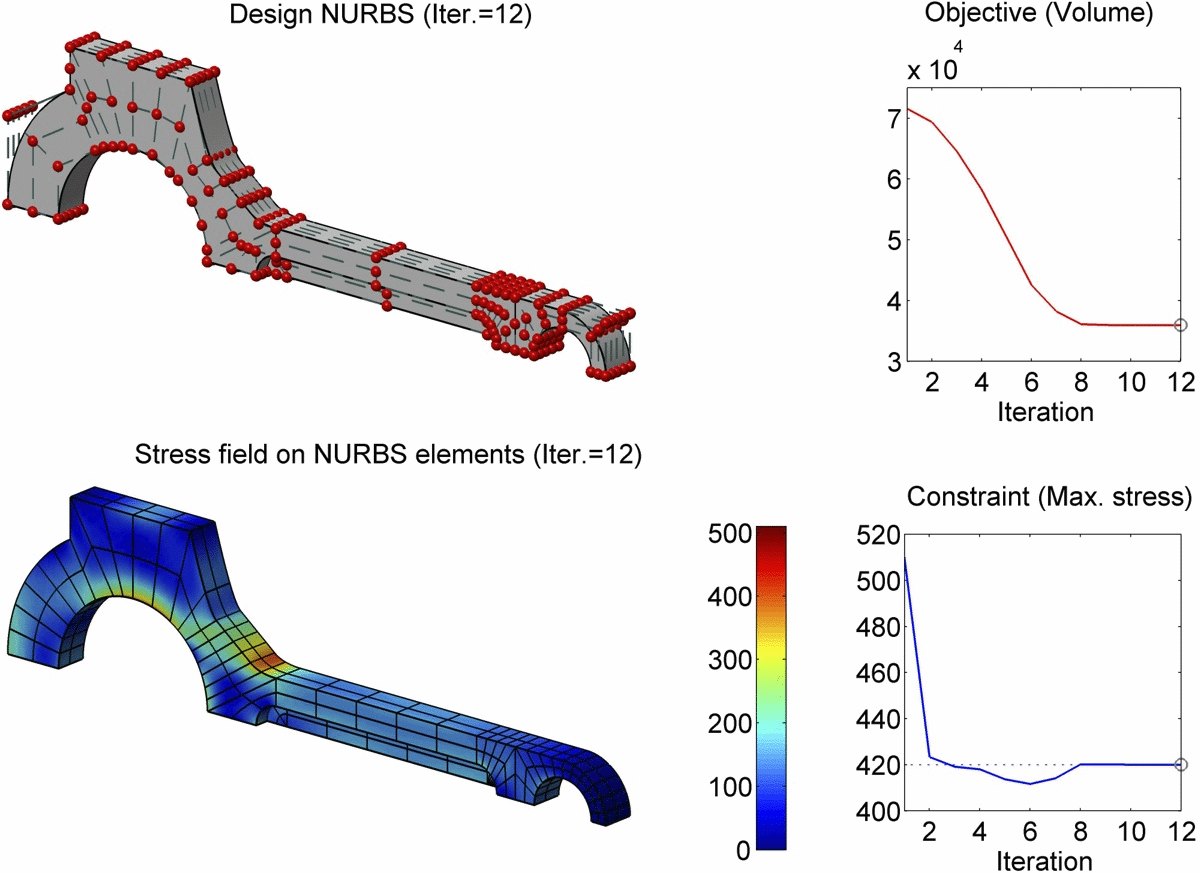
In this paper, we present a boundary integral based approach to isogeometric analysis and shape optimization. For analysis, it uses the same basis, Non-Uniform Rational B-Spline (NURBS) basis, for both representing object boundary and for approximating physical fields in analysis via a Boundary-Integral-Equation Method (BIEM). We propose the use of boundary points corresponding to Greville abscissae as collocation points. We conducted h-, p- and k-refinement study for linear elasticity problems. Our numerical experiments show that collocation at Greville abscissae leads to overall better convergence and robustness. Replacing rational B-splines with the linear B-Splines as shape functions for approximating solution space in analysis does not yield significant difference in convergence. For shape optimization, it uses NURBS control points to parameterize the boundary shape. A gradient based optimization approach is adopted where analytical sensitivities of how control points affect the objective and the constraint functions are derived. Two 3D shape optimization examples are demonstrated. Our study finds that the boundary integral based isogeometric analysis and optimization has the following advantages: 1) the NURBS based boundary integral exhibits superior computational advantages over the usual Lagrange polynomials based BIEM on a per degree-of-freedom basis; 2) it bypasses the need for domain parameterization, a bottleneck in current NURBS based volumetric isogeometric analysis and shape optimization; 3) it offers tighter integration of CAD and analysis without model conversion since both the input and output geometric model for analysis and optimization are the same NURBS surfaces.