Abstract

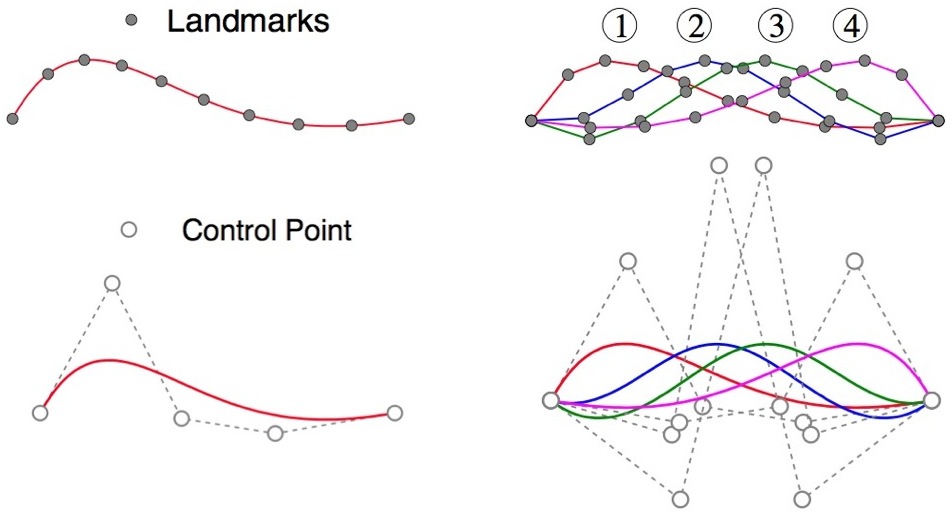
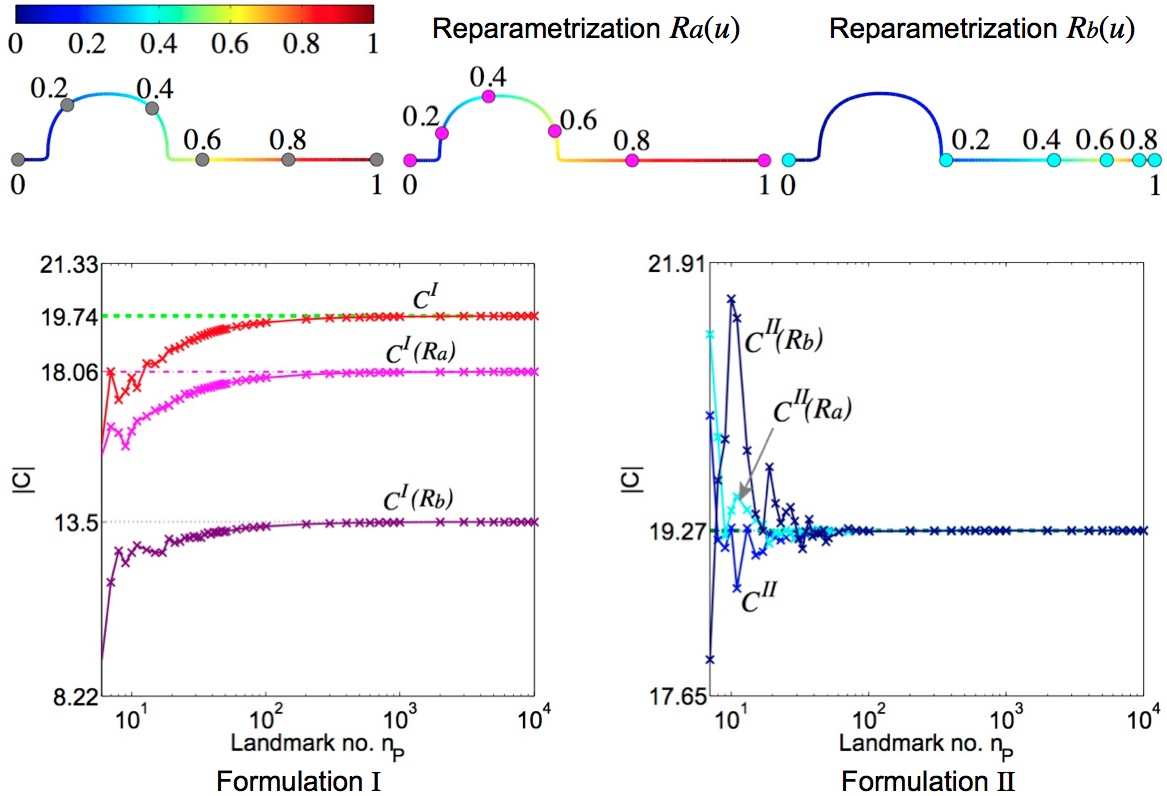
Computing the covariance matrix of a population of shapes is essential for establishing shape correspondence, identifying shape variation across the population, and building statistical shape models. The covariance matrix is usually computed from a discrete set of points (a.k.a. landmarks) sampled on each shape. The distribution and density of the sampled points thus greatly influence the covariance matrix and its spectral decomposition. In order to understand and overcome such dependency on point sampling, in this paper, we develop accurate and efficient methods for directly computing continuous formulations of the covariance matrix. We adopt B-splines both as a shape representation and as a form of reparameterization. We apply B-splines into two continuous formulations for computing the covariance matrix of shapes. We develop both analytical and efficient numerical methods for computing such matrices. In both formulations, the covariance matrix from the corresponding numerical approximation converges to the matrix from the continuous formulations when the number of sampled points in each shape becomes sufficiently large. Their applications in optimizing shape correspondence via minimizing the description length of a set of shapes is presented.