Overview

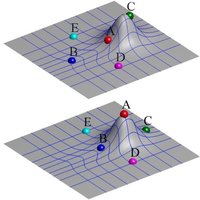
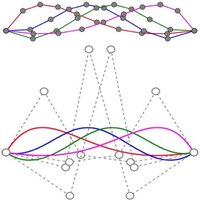
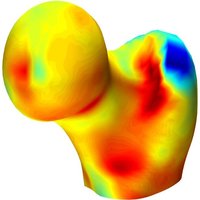
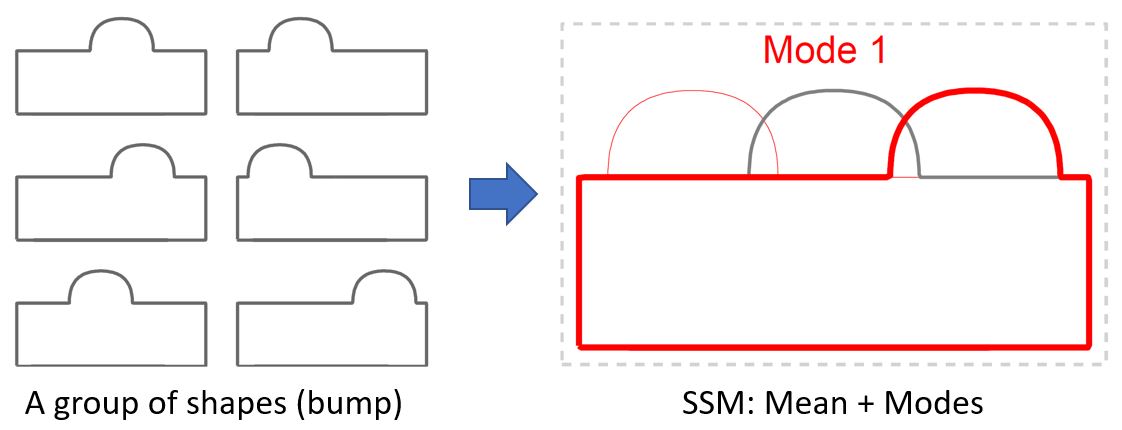
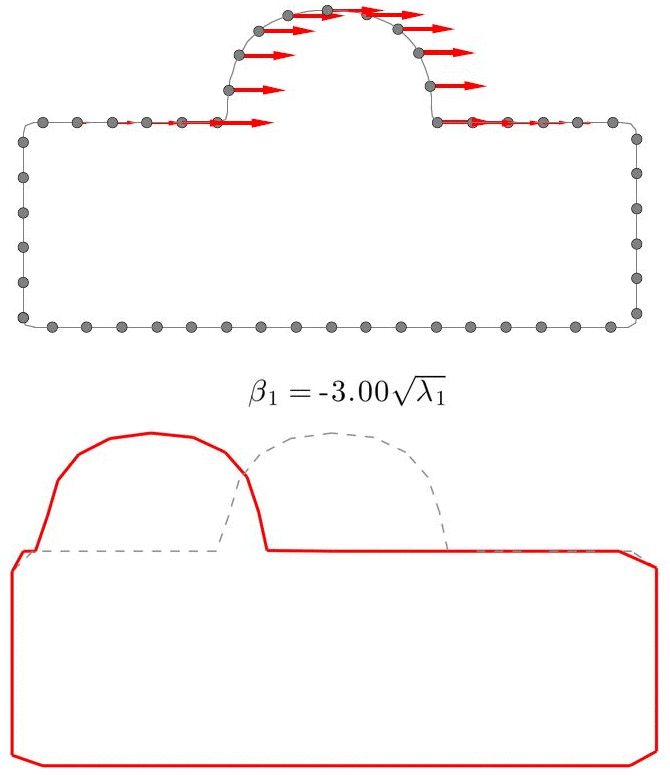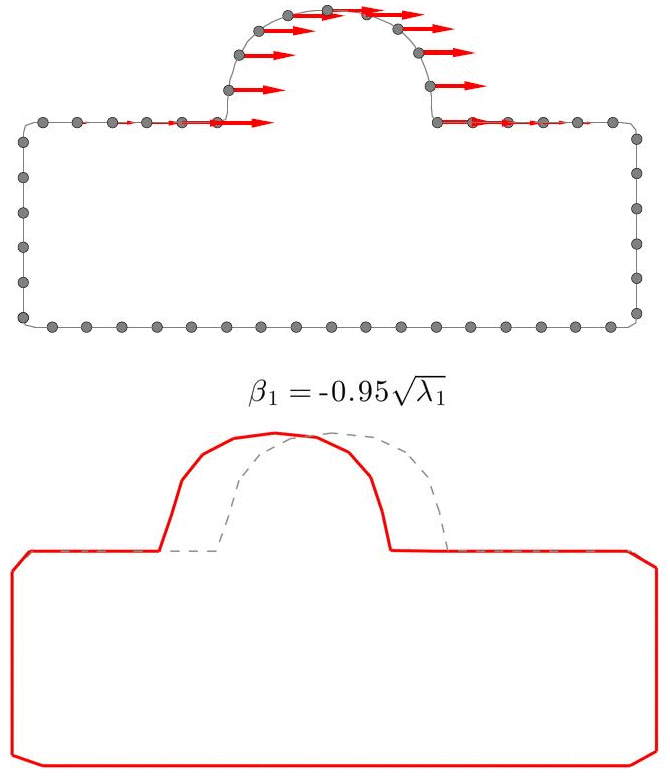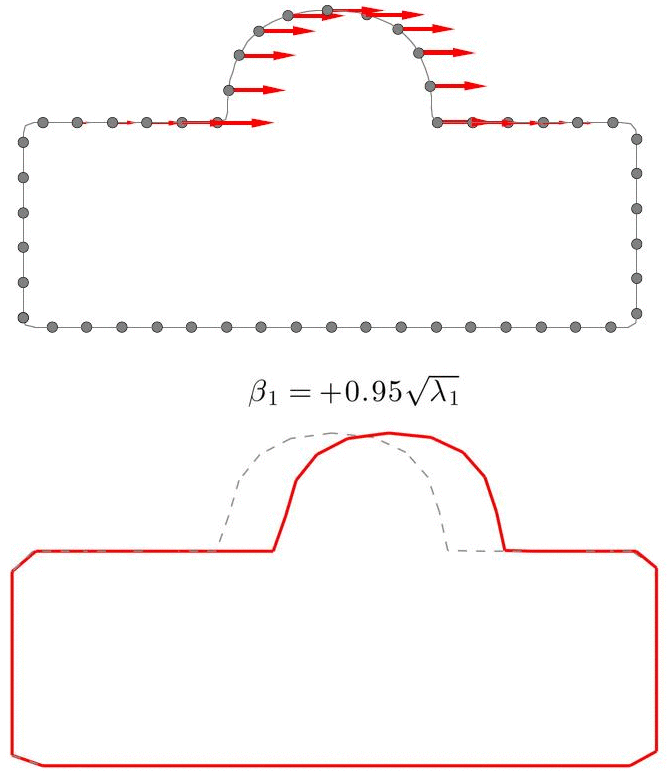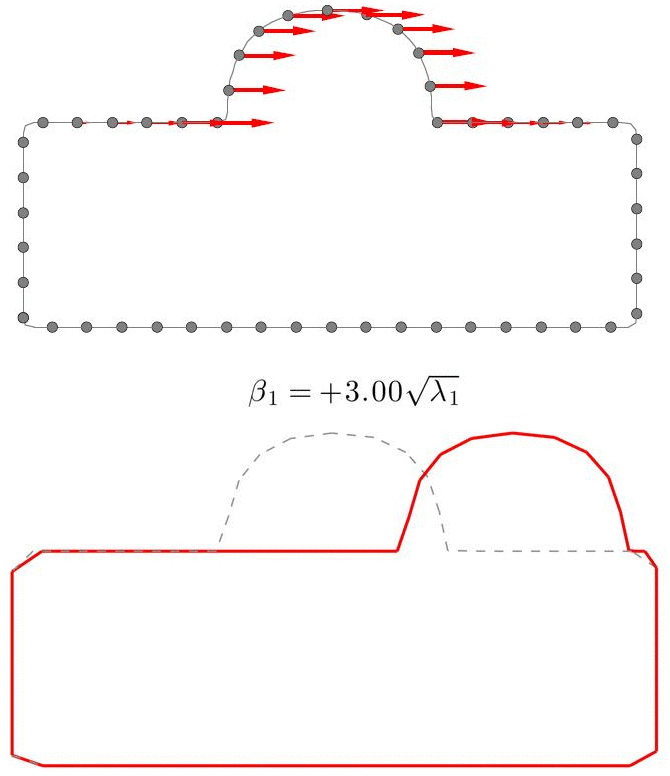
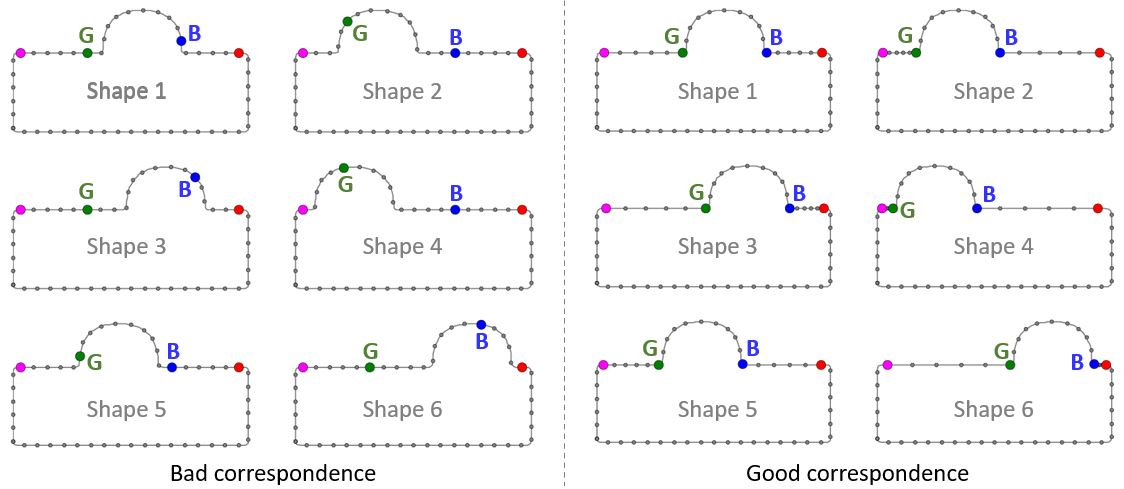
A Statistical Shape Model (SSM) serves as a compact characterization of the shape variation pattern in a group of shapes (training set). Initially it was used for the automation of image segmentations, and then it has been employed in a great variety of other applications such as pattern recognition, computer animation and medical diagnosis etc. Building SSM reduces to searching for correspondence across the entire training set shape instances. The population-based approach formulates the search as an optimization problem that minimizes a measure (e.g. Description Length) of resultant SSM, and gives correspondence and SSM of desirable quality. During optimization, the correspondence updates are achieved by reparameterizing shapes in the parameter space.

Previously, the reparameterization function is modeled by concatenating a large number of local warps, leading to extremely inefficient iterations and huge time cost. We propose a direct representation of the reparameterization function by B-splines, develop associated diffeomorphism conditions and derive fast gradient formula by adjoint method. Both synthetic examples and real medical applications have confirmed the effectiveness of proposed algorithm and the efficiency advantages. As a key mathematical entity in the statistical modeling and correspondence optimization, the covariance matrix is also studied in the context of both discrete and continuous representation of shape instances.

We are very thankful to the National Science Foundation for the following grants:

- Award #0900597  Direct Digital Design and Manufacturing (D3M) from Massive-Point-Cloud Data
- Award #1030347  Direct Measurement from Scan Data with Adaptive Moving Least-Squares Surfaces under Controlled Spatial Dependency