Overview

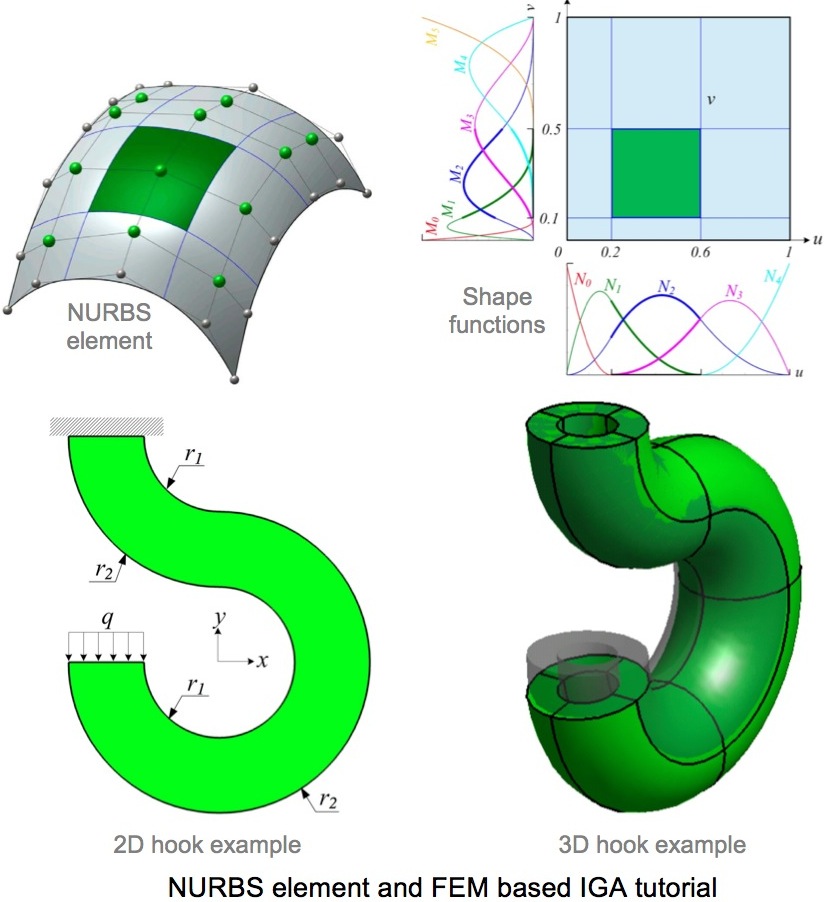
Compared to conventional FEA (Finite Element Analysis), isogeometric analysis (IGA) uses the same basis functions that represent geometry (usually CAD models) for approximating physical fields in analysis. This closer integration of CAD and FEA greatly alleviates the burden of converting CAD geometry to analysis-ready models. As the standard geometric form in CAD systems, basis functions generated from NURBS (Non-Uniform Rational B-Spline), are employed to construct an exact geometric model. Convergence study on plenty of examples shows that NURBS basis function based FEA exhibits superior computational advantage to its traditional counterpart --- Lagrange polynomials based FEA.

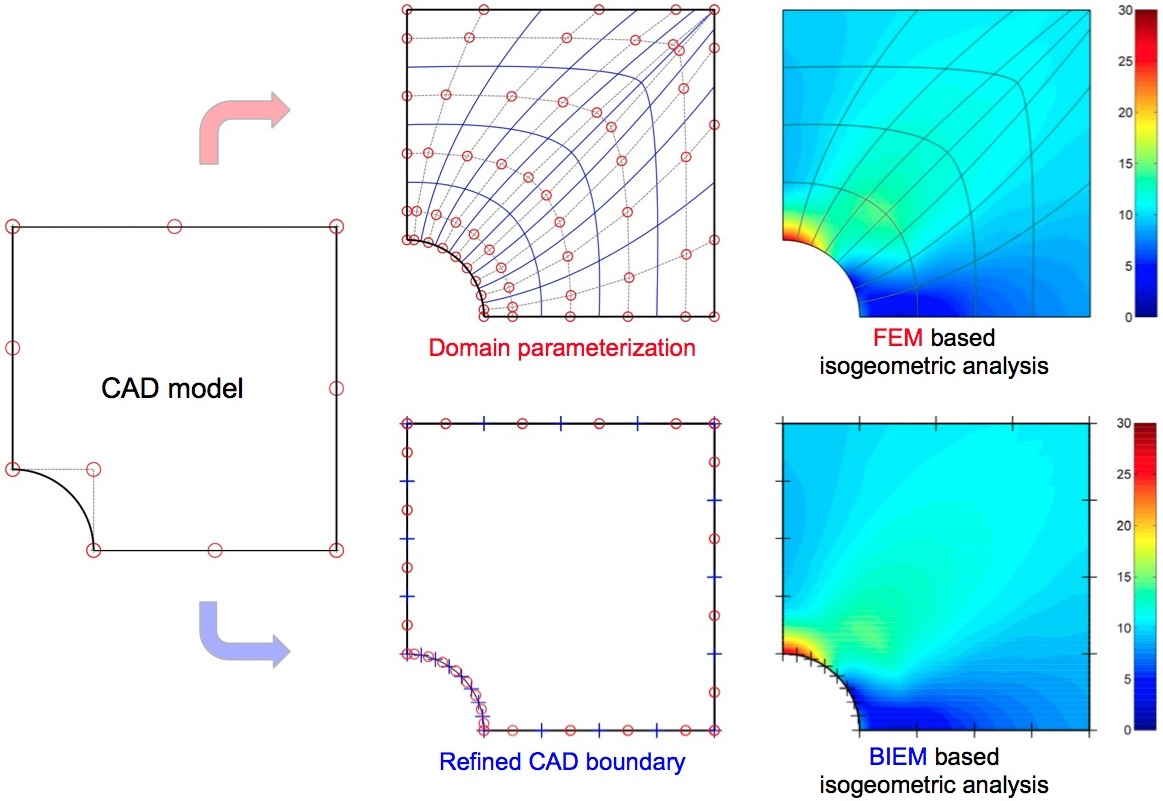
Despite the performance improvements due to choosing NURBS basis functions over Lagrange polynomials, analysis framework using Finite Elements (FEM) is unable to avoid the expensive domain parameterization. Since CAD models are represented by boundaries (B-Rep) in NURBS, we explore the Boundary Integral Equation Method (BIEM) based isogeometric analysis, which requires only the NURBS boundary. Analysis examples show further computational advantage of BIEM-IGA to FEM-IGA, and the proposed techniques are also utilized for shape optimization.

We are very thankful to the National Science Foundation for the following grants:

- Award #0900597  Direct Digital Design and Manufacturing (D3M) from Massive-Point-Cloud Data
- Award #0900170  GOALI/Collaborative Research: Understanding and Controlling Variation Propagation in Periodic Structures: From Geometry to Dynamic Response
- Award #1030347  Direct Measurement from Scan Data with Adaptive Moving Least-Squares Surfaces under Controlled Spatial Dependency