| 上一项 | 下一项 |
统计形状建模
伊利诺伊理工大学
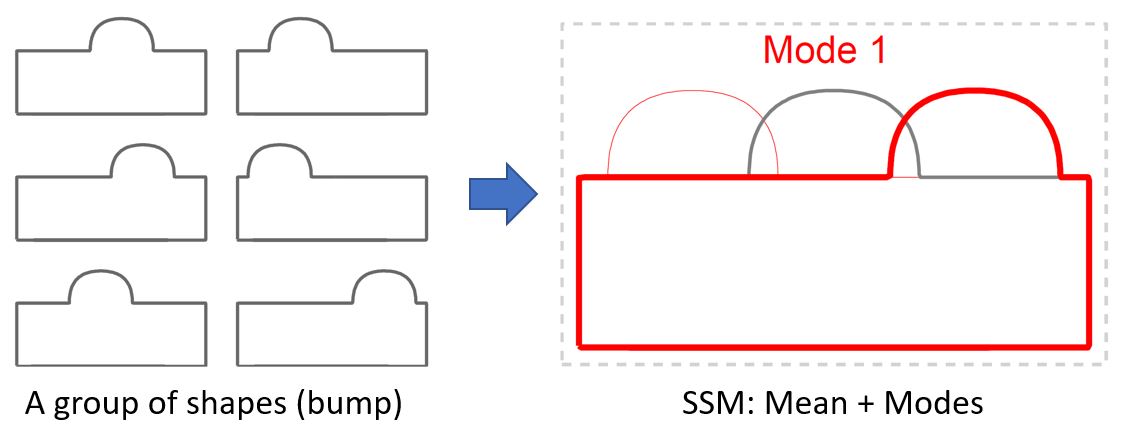
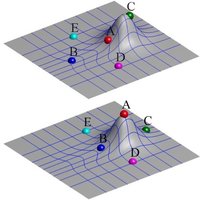
一组形状的统计模型(SSM)的基本含义如上图中的简单例子所示。假设有一组形状,唯一的区别就是半圆形凸起在上边的水平位置不同。如果有右上图中的统计模型,其模态1刚好捕捉到此水平位置变化模式,则组内任意形状都能很容易很方便地由此统计模型表示。
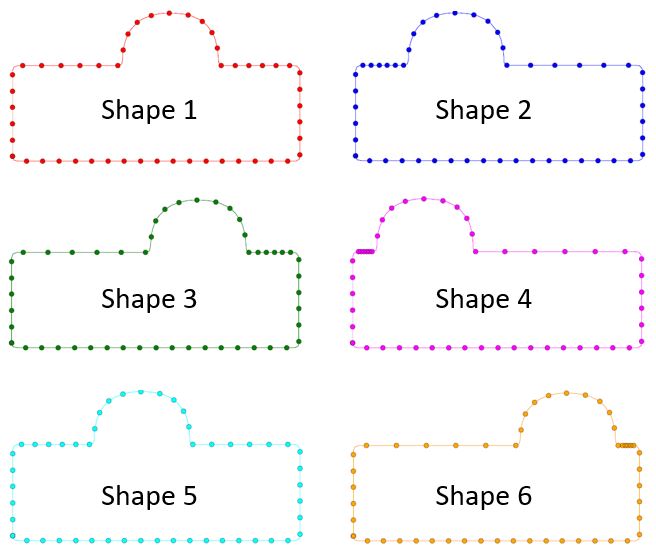
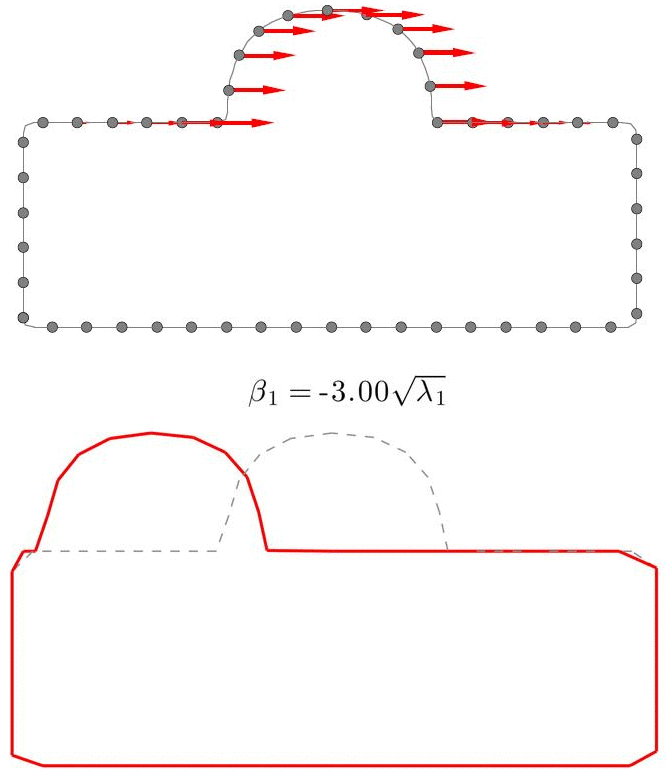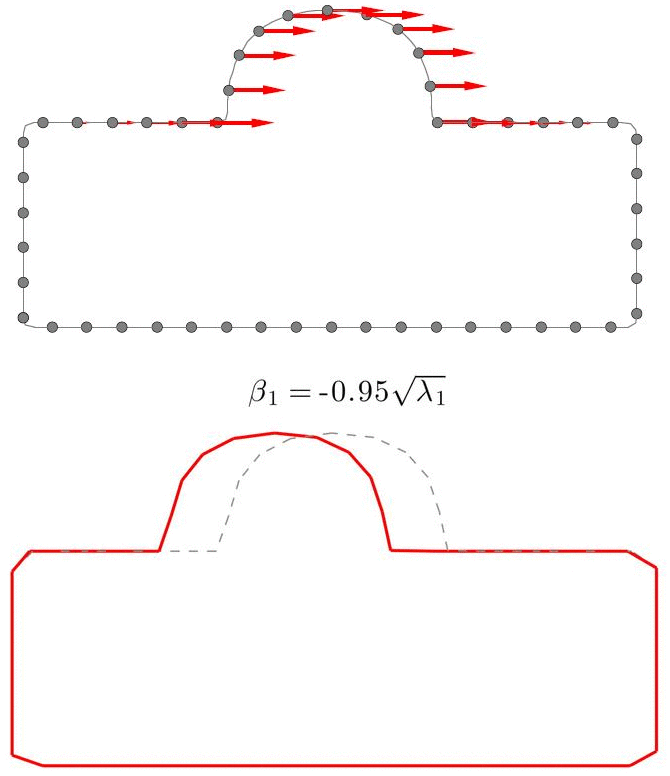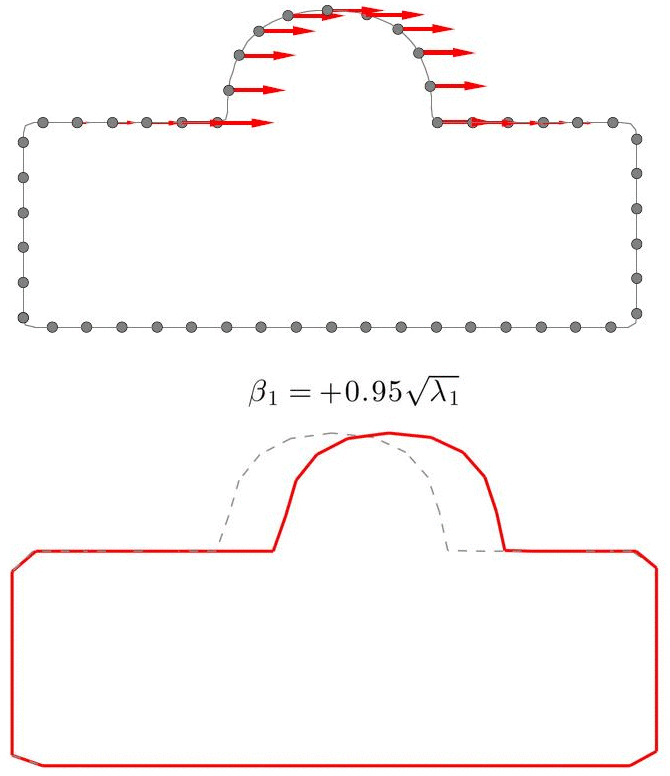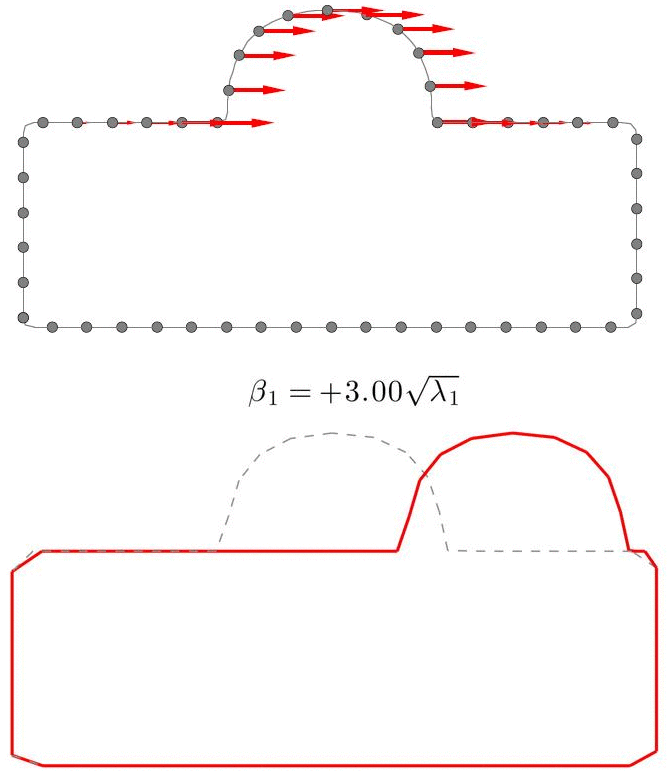
为了获得一组形状(训练集)的统计模型,需要在所有形状上采同样数目的点,算出协方差矩阵,然后得到统计模型,即平均值形状和各模态。上图为一种采样方式的50个点所生成的统计模型,可见其模态1为凸起水平位置的变化。
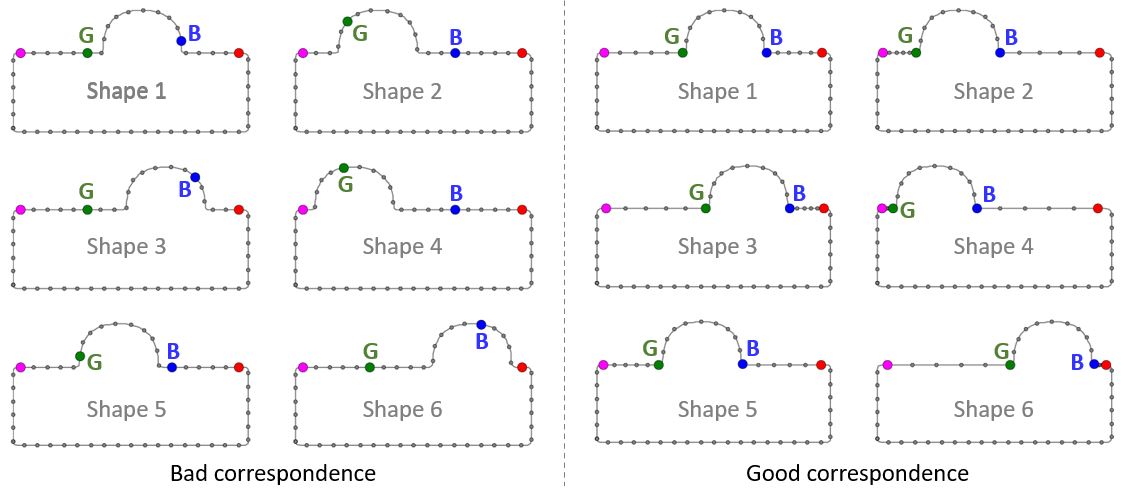
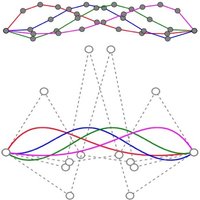
显然,不同的采样方式会生成不同的SSM,而且采样状态本身就定义了组内各形状之间的几何特征是如何一一对应的,即“形状对应”。上面显示了两种不同采样的方式,也即两种不同的形状对应状态。直观上能判断出,左边的对应状态差,右边的好。观察绿色和蓝色的指示点就容易看出,左边的对应中,凸起半圆的两端角落根本没有对应起来,而右边则是十分整齐的对应着。

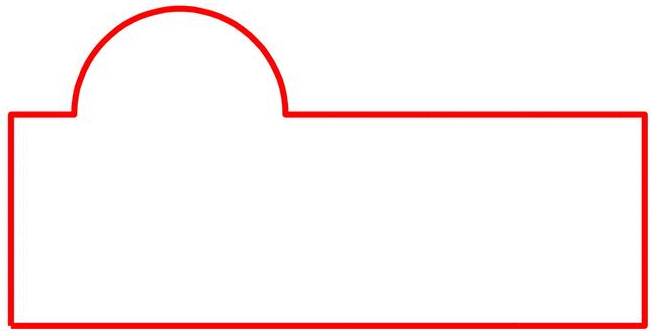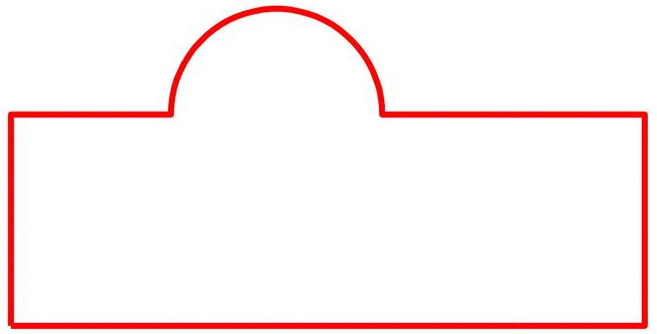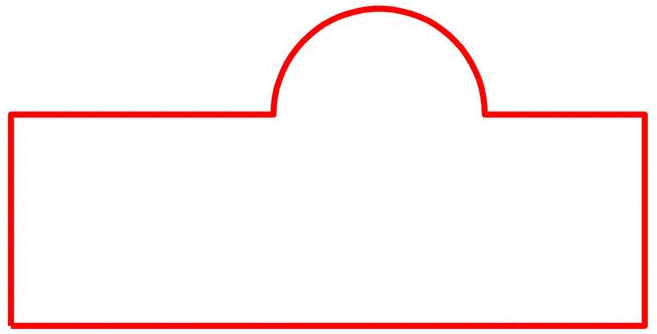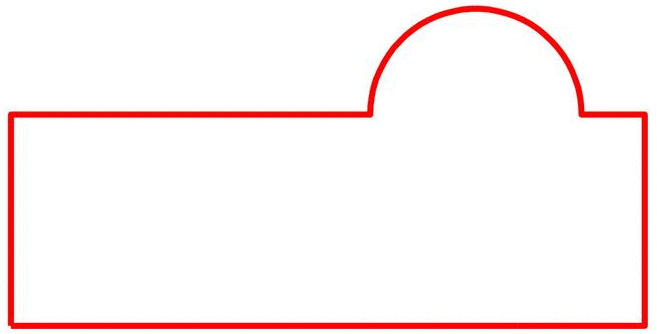
实际上,任何对应状态下的形状都能生成相应的统计模型,只不过其质量和可用性就不得而知了。而只有好的对应状态下生成的模型才能准确反应形状组的变化特征从而有实际作用。上图不难看出,对应差的状态下生成的左边的SSM根本无法捕捉到任何有用的变化模式,而对应质量好的状态下的右边的SSM反应了正确的水平位置变化模式。由此可见,SSM的关键问题就是求解形状对应的最优状态,而这可以通过优化方法来解决。
项目概述
一组形状(训练集)的 “统计模型”(SSM)能够精简地表达组内形状的变化模式。统计模型最初用于图象自动分割,随后又在模式识别,计算机动画和医疗诊断等领域获得了十分广泛的应用。创建统计模型归结为搜寻所有形状的对应状态,进而又转为一个优化问题,其目标函数是形状对应质量的度量。在优化迭代的过程中,形状对应状态的更新是通过在参数域内的重新参数化实现的。
重参数化此前是由大量的局部调节叠加而成,因而十分低效耗时。为此我们提出一种用B样条曲线曲面直接表达重参数化的方法,并且推导出微分同胚条件和快速梯度导数的伴随灵敏度公式。通过人造问题和医学领域中的实际问题实验,我们发现此新方法即能解决统计建模的优化问题,而且相当高效。由于协方差矩阵是统计建模和形状对应优化问题中一个关键的数学概念,我们专门对其在连续和离散域内的特性做了研究。
最后非常感谢美国国家科学基金会提供的以下赞助:
项目编号#0900597 大规模点云数据的直接数字化及设计制造
项目编号#1030347 使用自适应移动最小二乘曲面满足可控空间约束条件对扫描数据的直接测量