| 上一篇 | 下一篇 |
结果展示
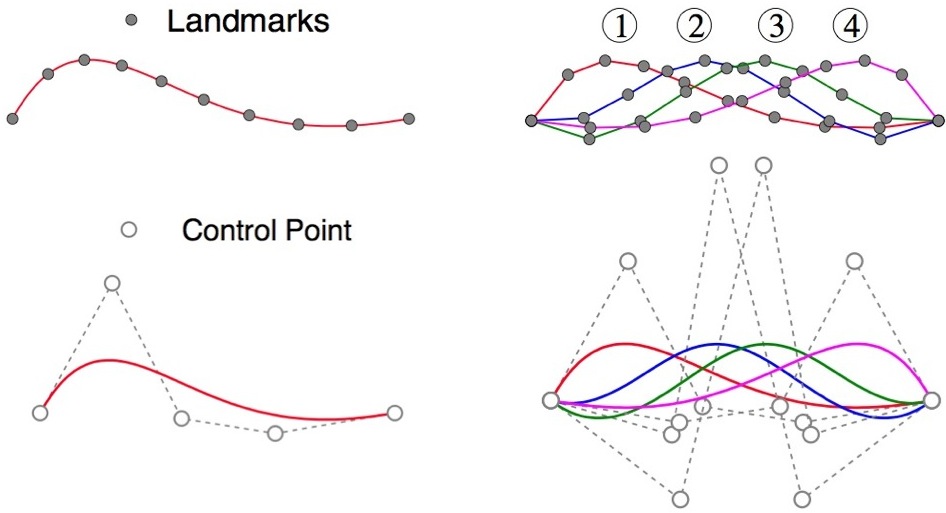
为了计算“线凸起”曲线形状组的协方差矩阵,有两种方式可以表示形状曲线:离散域(第一行)和连续域(第二行)。对离散表达方式使用标记点采样,而对于连续表达可以用B样条曲线。
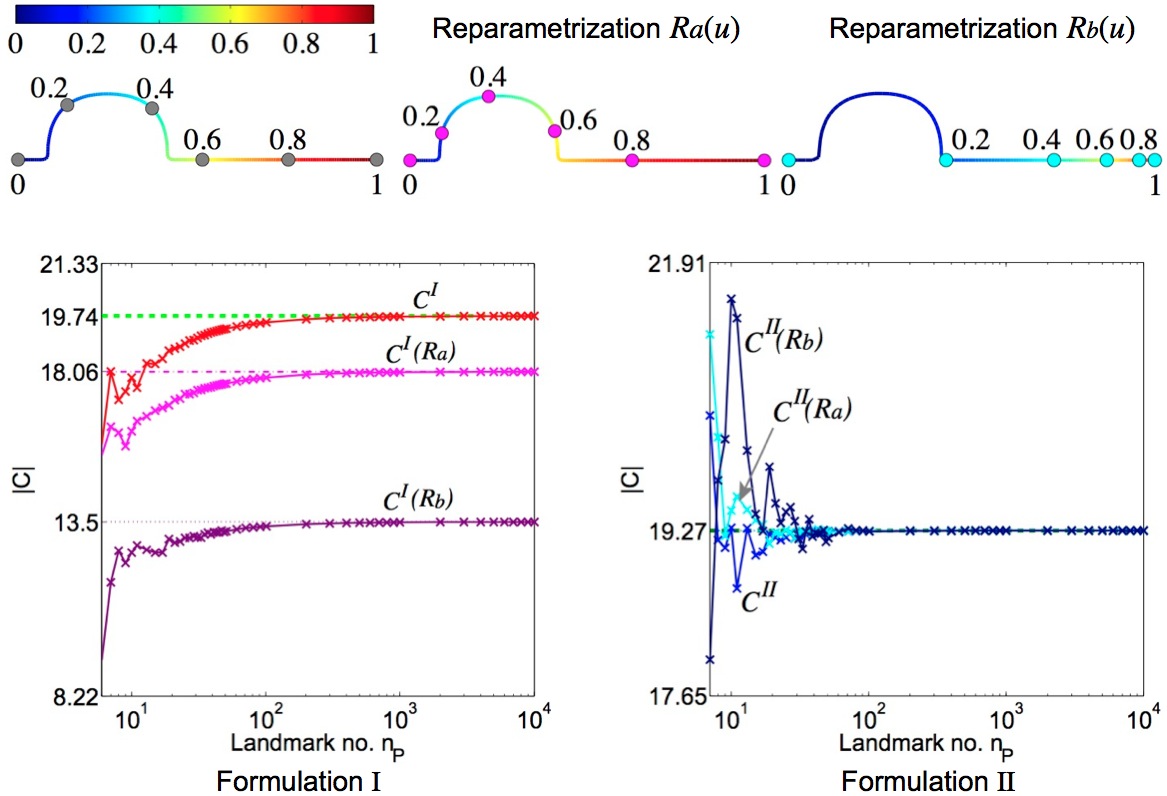
上图第一行显示了三种不同的参数化方式:原始参数化,叠加重参数化Ra(u),叠加重参数化Rb(u)。三种方式搭配两种连续公式I and II都可以计算出相应的协方差矩阵。上图第二行给出了对协方差矩阵求弗罗贝尼乌斯范数结果:1)离散表达收敛于相应的连续表达值;2)公式I在三种不同参数化下收敛于不同值;3)公式II在三种不同参数化下收敛于同一值,即不依赖于参数化。
论文摘要
一组形状的协方差矩阵计算对于确立形状对应,捕捉变化模式以及统计建模来说都至关重要。协方差矩阵通常都是通过在形状上采样出一些离散的点(标记点)来计算的。标记点采样的分布和密度都会极大地影响协方差矩阵和特征分解特性。为了理解和克服这一对采样的依赖关系,我们提出了一种基于连续形状表达无需采样直接计算协方差矩阵的高效方法。其连续形状表达以及重参数化都使用B样条形式。连续形状表达有两种公式可选。我们提出了解析方法和高效数值方法来计算协方差矩阵。两种公式计算的协方差矩阵显示,在采样点无穷多时数值方法都收敛于解析值。最后我们展示了如何利用这样的计算方法来求解以“描述长度”为目标函数的形状对应优化问题。