| 上一项 | 下一项 |
等几何计算方法
伊利诺伊理工大学
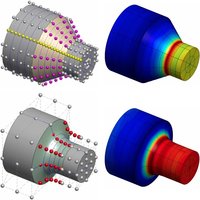
大部分CAD系统通过边界表达(B-Rep)来储存模型几何数据并且以非均匀有理B样条(NURBS)作为几何格式;这就是说在CAD系统里面,边界曲面NURBS数据可供直接使用。传统的等几何分析(IGA),即基于有限单元法(FEM)的IGA,必须要进行十分耗时繁琐的实体“内部NURBS参数化”。为了避免这个低效过程,我们在现有的NURBS边界上利用边界积分法(BIEM)做等几何分析,即基于BIEM的IGA。数值实验表明,BIEM-IGA不仅完全省去了内部参数化中间过程,而且得出的分析结果质量相比FEM-IGA毫不逊色。
项目概述
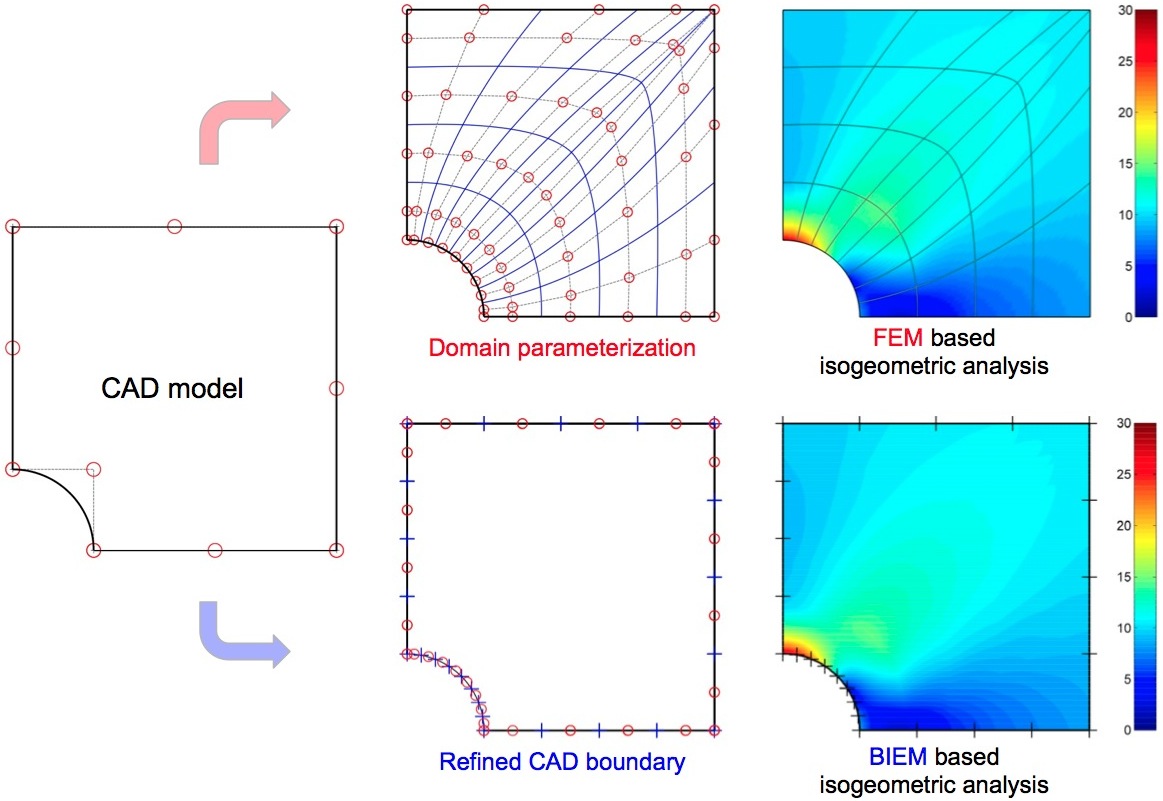
等几何分析(Isogeometric Analysis 或 IGA)用表达几何形状的基函数来拟合物理场;即几何模型和物理分析使用同一基函数,故而得其名。该计算方法实则计算机辅助设计(Computer-Aided Design 或 CAD)和有限单元分析法(Finite Element Analysis 或 FEA)的进一步紧密结合,极大地缓解了需要转化CAD几何模型为适宜分析模型的压力。 由于非均匀有理B样条曲线(Non-Uniform Rational B-Splines 或 NURBS)是CAD系统的标准几何形式,几何模型可以由NURBS的基函数精确表示。无数的收敛实验显示:基于NURBS基函数的有限元分析相比传统的拉格朗日基函数具有相当突出的计算优势。
相比IGA来说,传统的有限元分析的劣势显而易见,除了使用拉格朗日基函数以外,几何模型内部参数化也十分复杂耗费资源。考虑到表面或者边界的参数化容易许多,我们研究了如何使用边界积分法(Boundary Integral Equation Method 或 BIEM)结合等几何分析的NURBS基函数来避免内部参数化。实例表明,基于边界积分的等几何分析进一步提升了计算效率,并且十分适合用于形状优化。
最后非常感谢美国国家科学基金会提供的以下赞助:
项目编号#0900597 大规模点云数据的直接数字化及设计制造
项目编号#1030347 使用自适应移动最小二乘曲面满足可控空间约束条件对扫描数据的直接测量
项目编号#0900170 GOALI/协作研发:理解及控制周期性结构中的变化传导:从几何到动态响应
相关教程
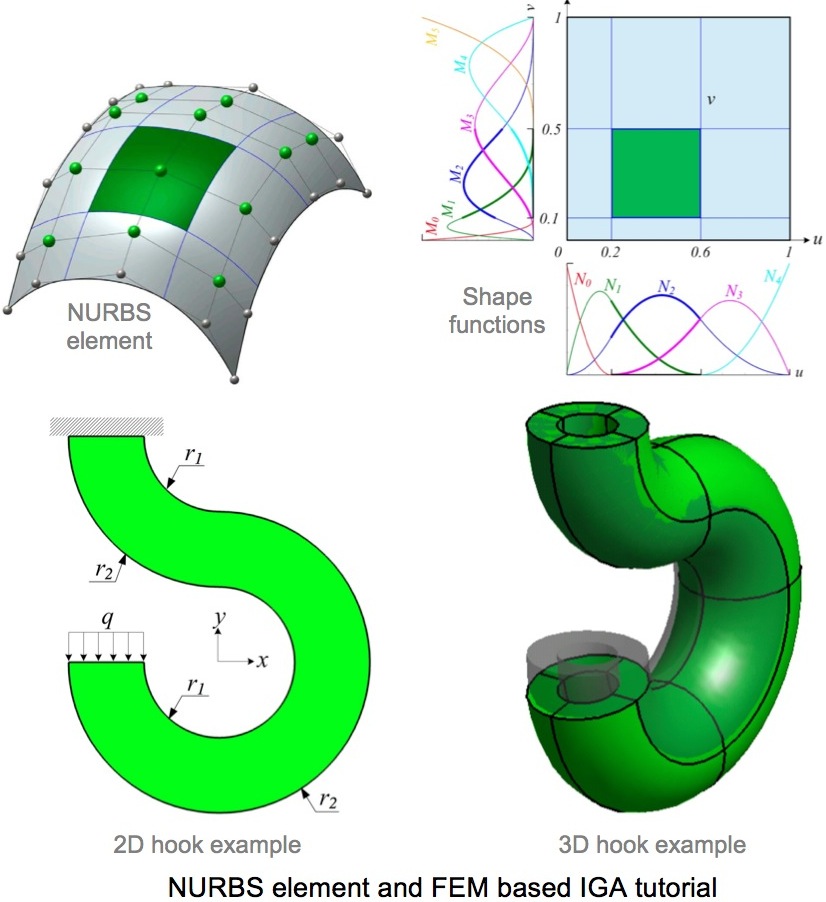
上图显示的NURBS曲面在物理域的曲面形态以及其在参数域内的基函数特性,可以帮助我们深入理解“等几何”的概念。此外,我们提供一个很小的计算实例(二维平面吊钩),来演示等几何有限元分析的详细计算步骤;附件中会提供关于NURBS模型的几何参数,有限单元划分,基函数,刚度矩阵,狄利克雷/纽曼边界条件等的所有细节。