| 上一篇 | 下一篇 |
Computer-Aided Design 期刊, 43(11), 2011年
亦发表于SIAM/ACM on Geometric Design & Solid and Physical Modeling (GD/SPM) 联合会议特刊，2011年10月
GD/SPM 2011 最佳论文一等奖
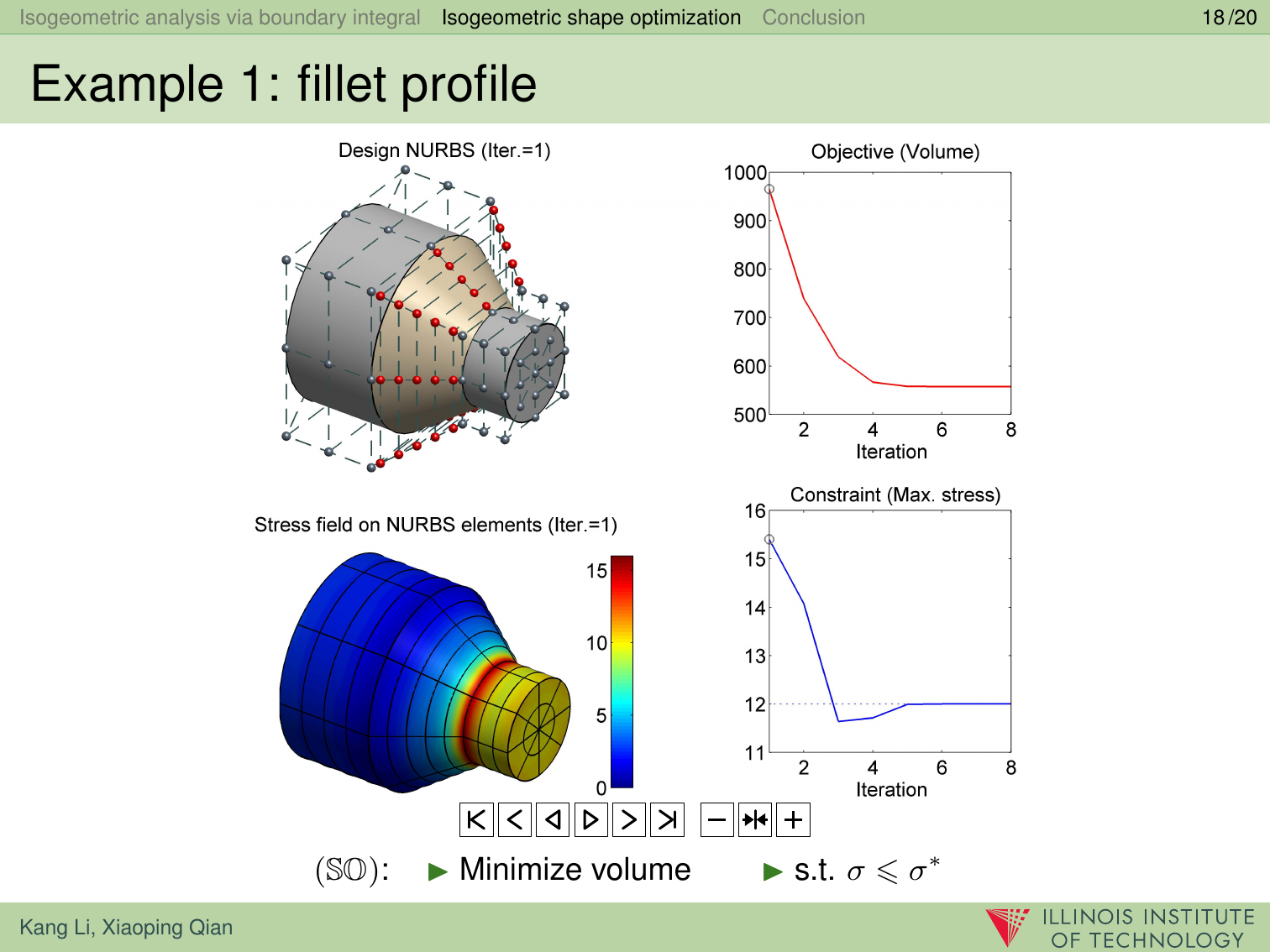
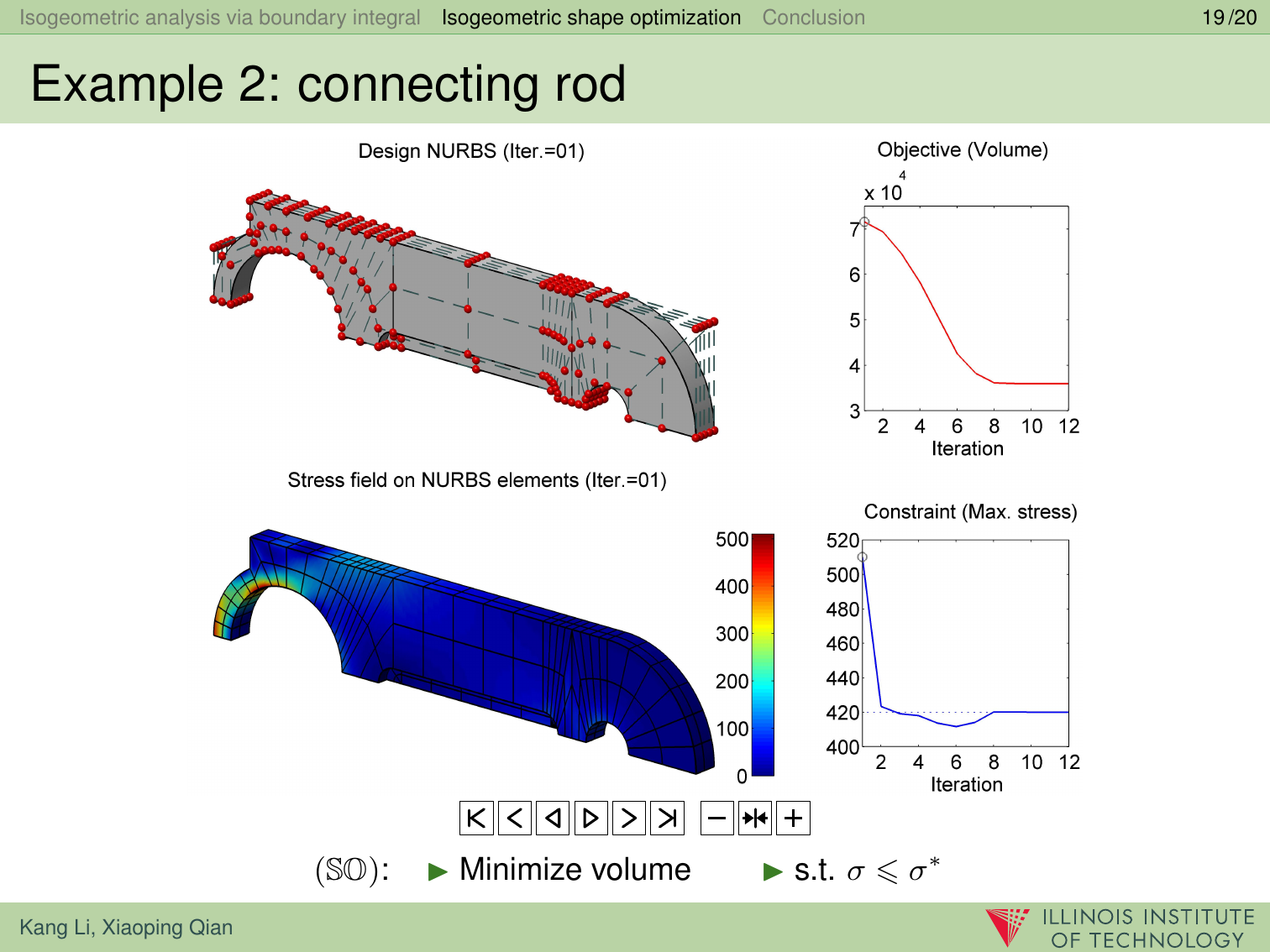
结果展示
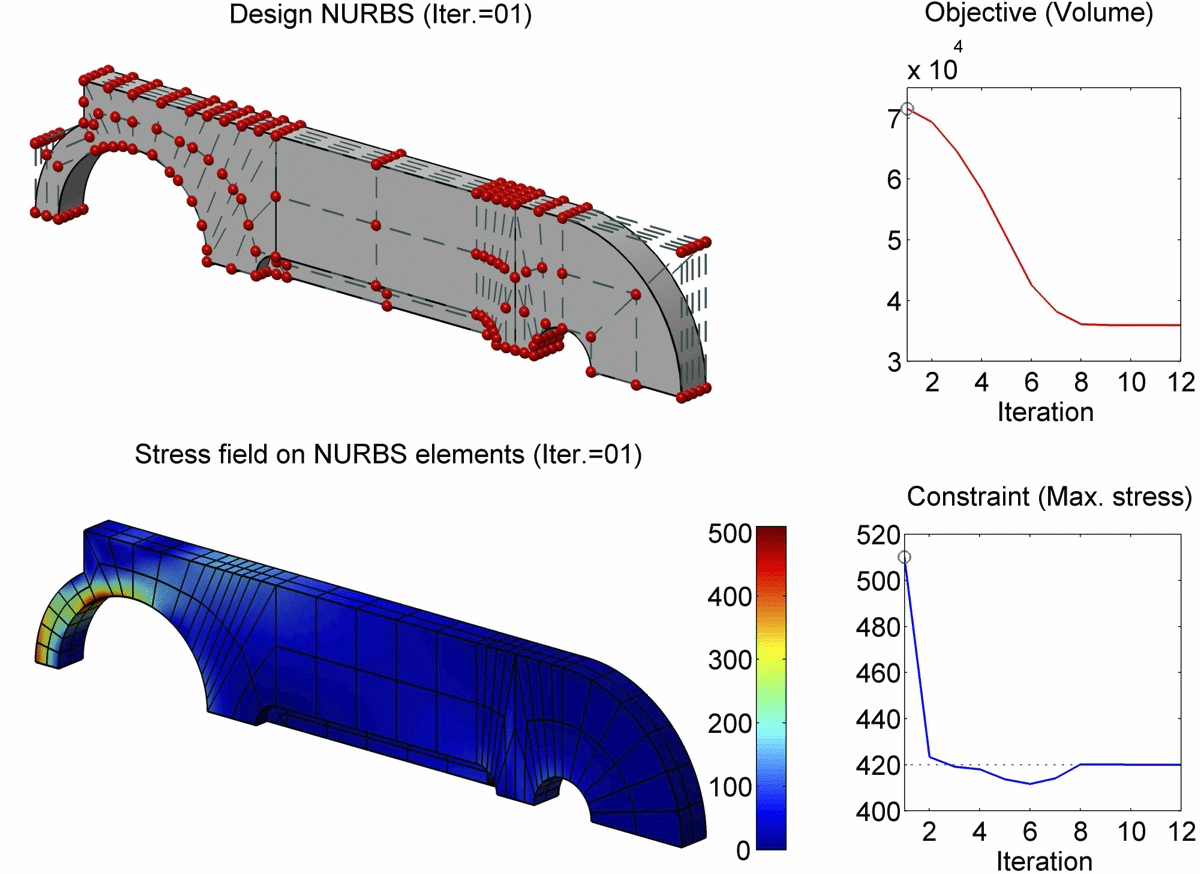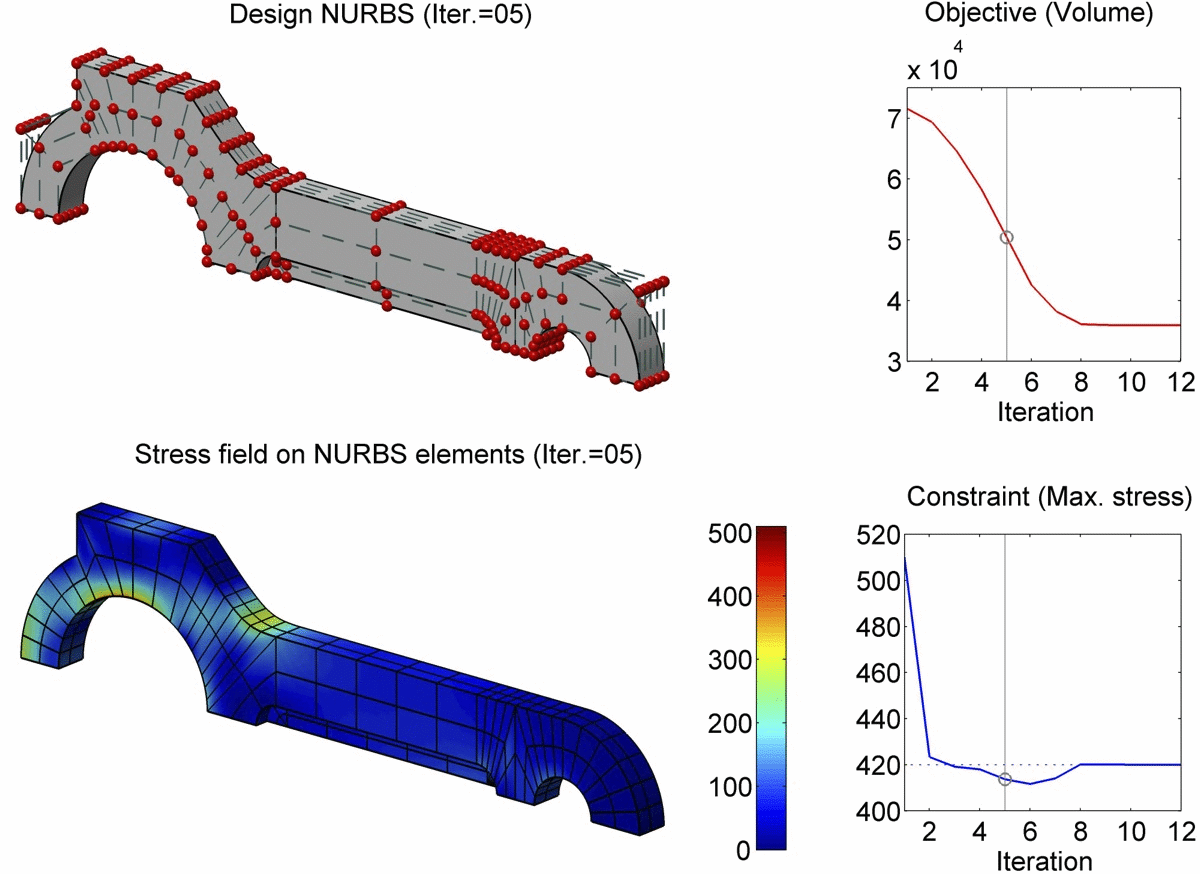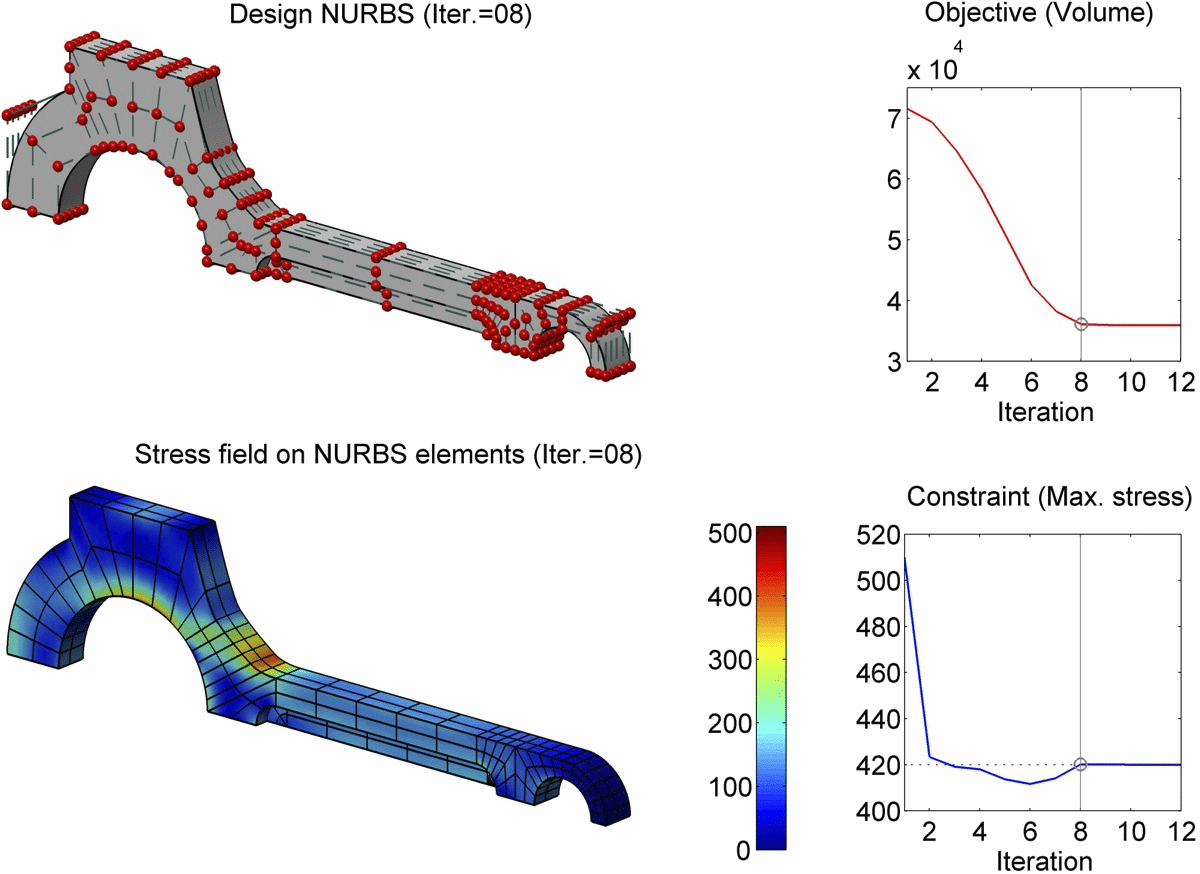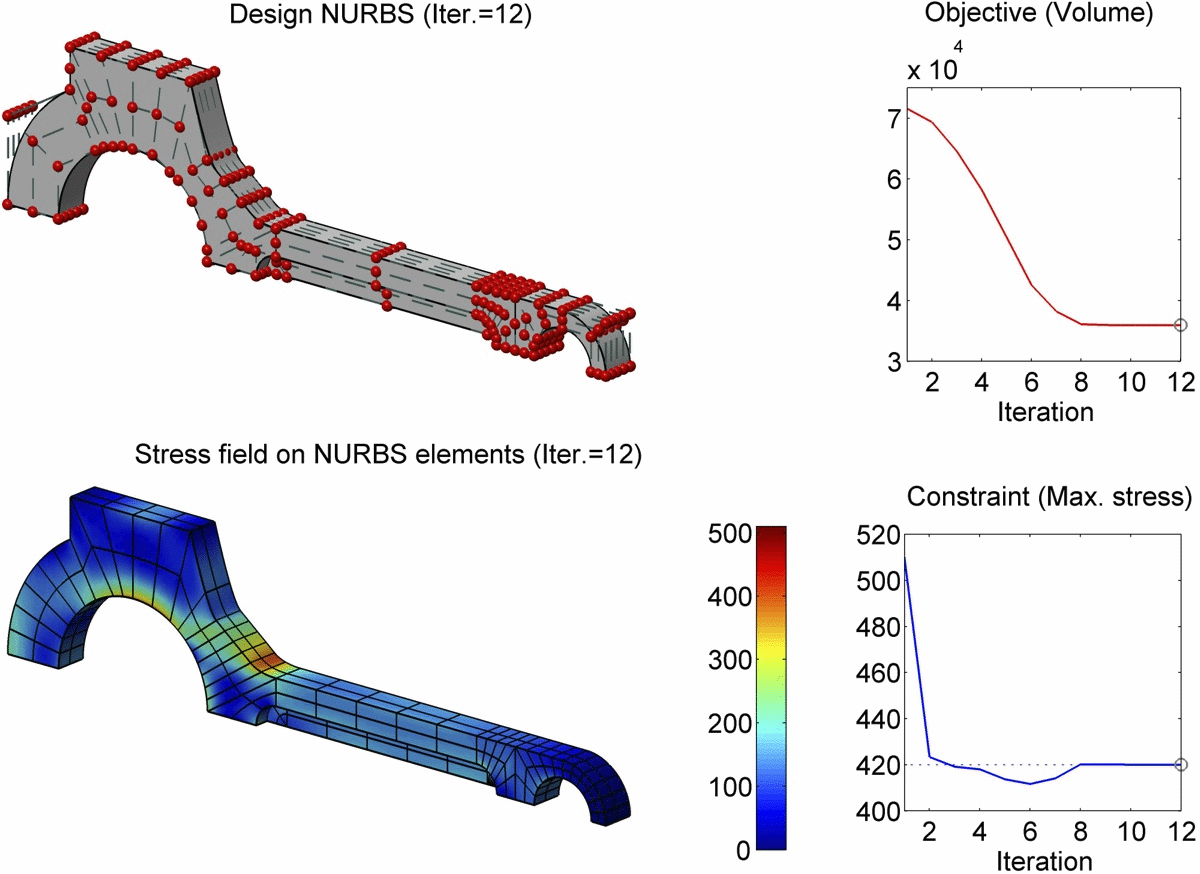
如上图所示，文中提出的基于边界积分公式(Boundary Integral Equation 或 BIE)的等几何分析方法（IsoGeometric Analysis 或 IGA）用于求解轴向承重的三维倒角形状优化问题。模型由5块NURBS曲面片构成，共划分为128个NURBS边界单元用于边界表达和分析。在经过优化求解的7次迭代历之后，三维倒角实体的体积达到最小值，同时所受最大应力值也从15.2降至12。
在上图所示的连杆形状优化问题中，模型的边界由22块NURBS曲面片构成，共划分为382个NURBS边界单元。在经过优化求解的22次迭代历之后，连杆体积达到最小值，同时所受最大应力也从510Mpa降至420Mpa。
论文摘要
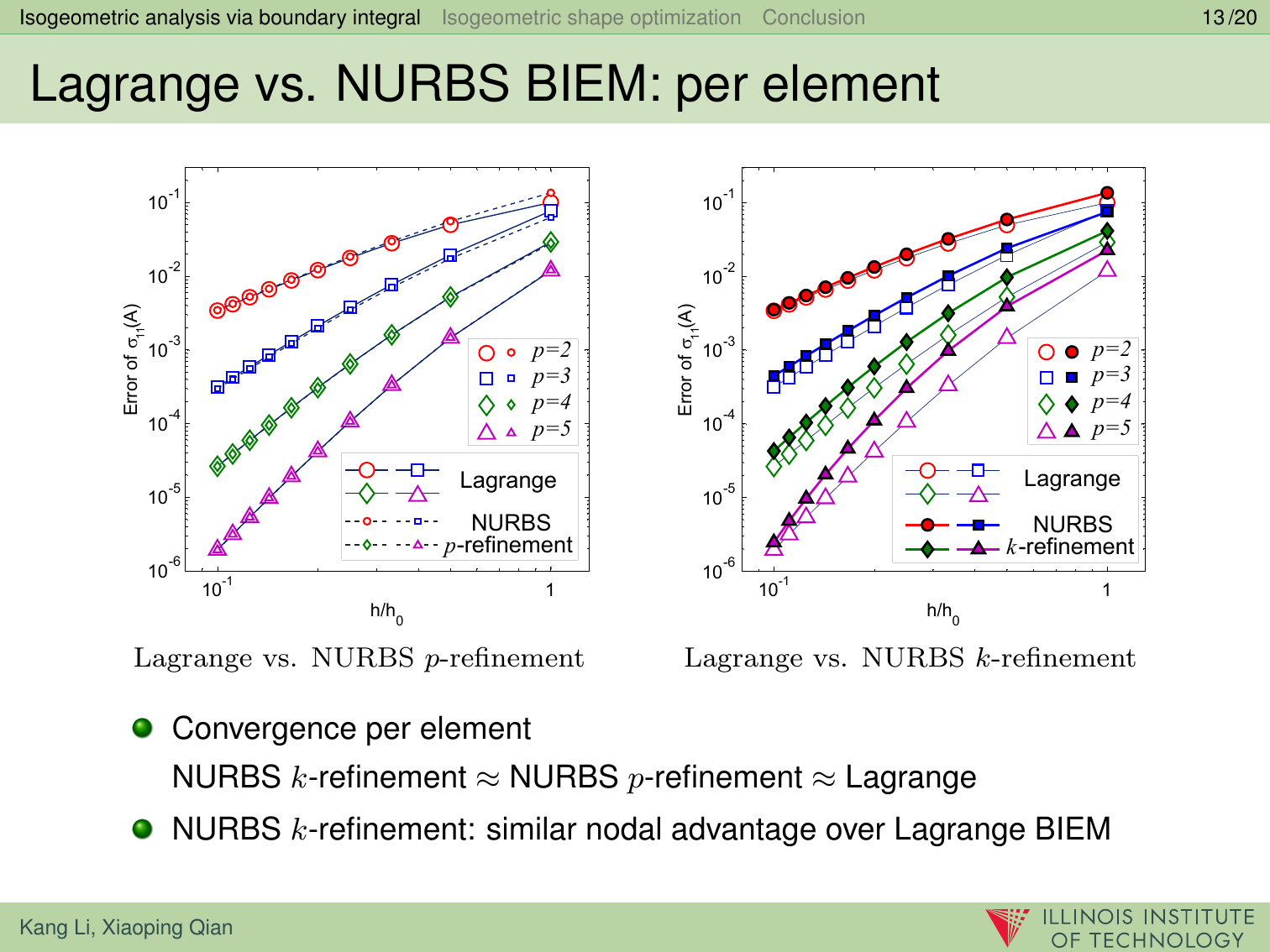
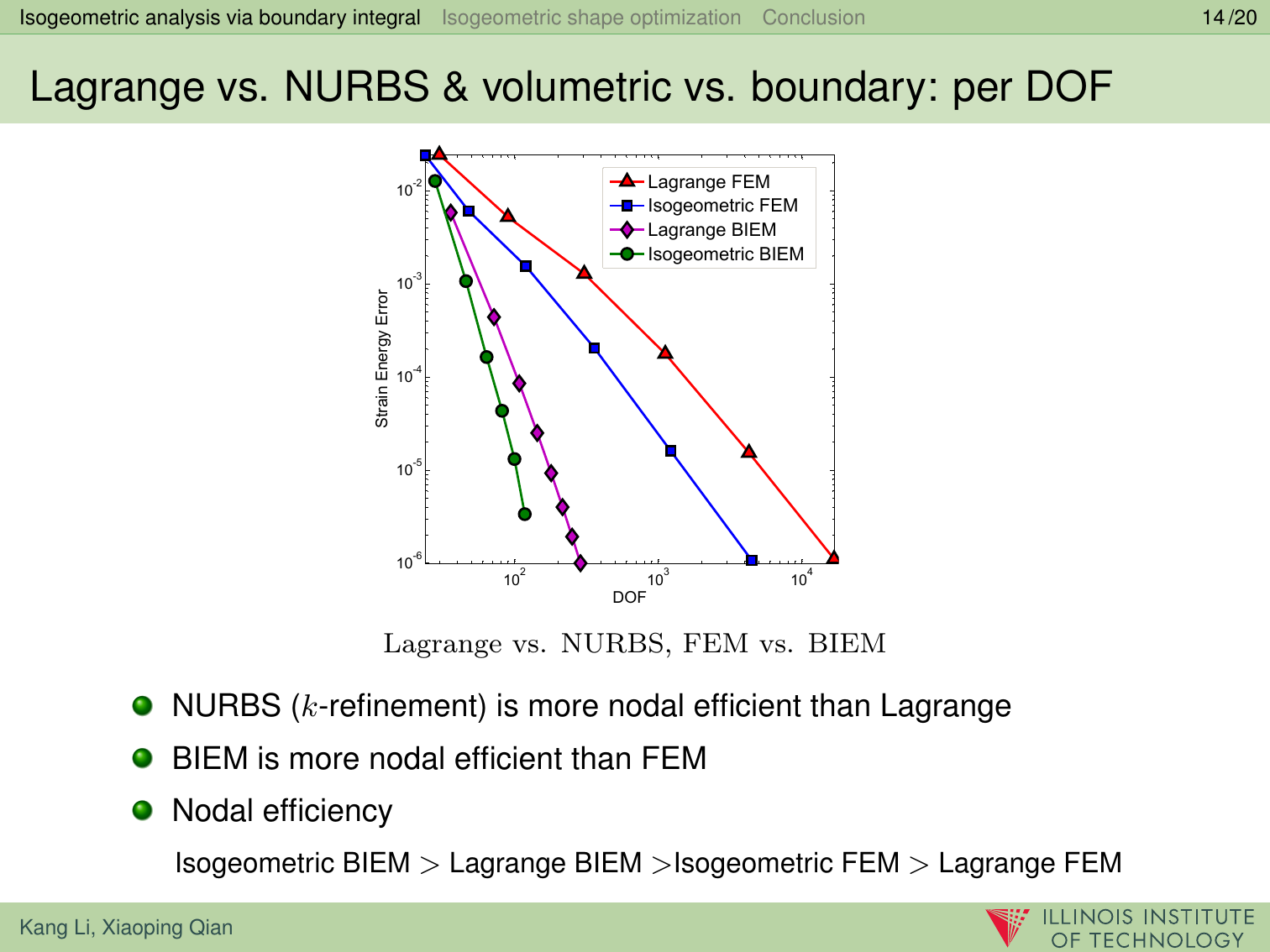
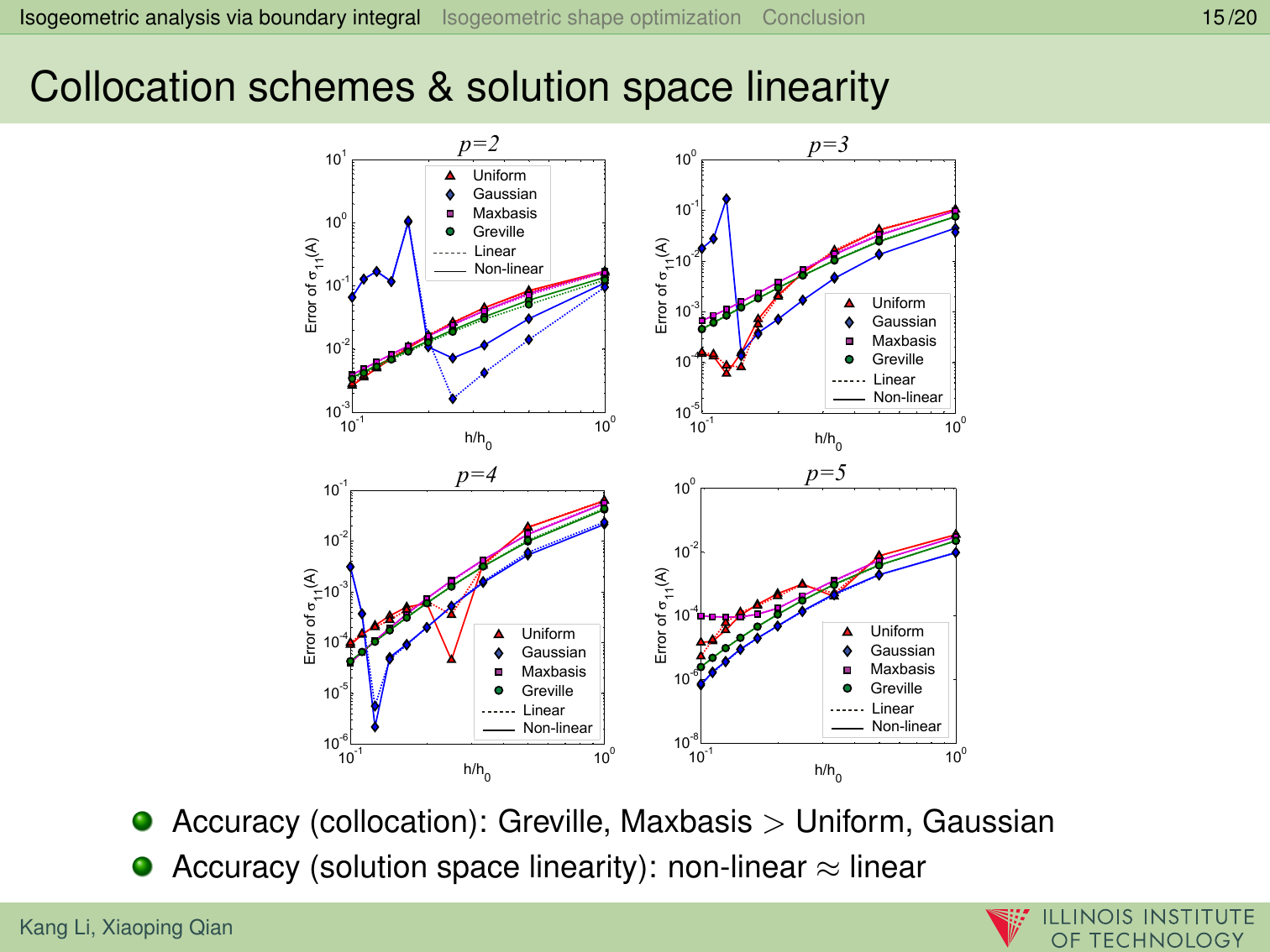
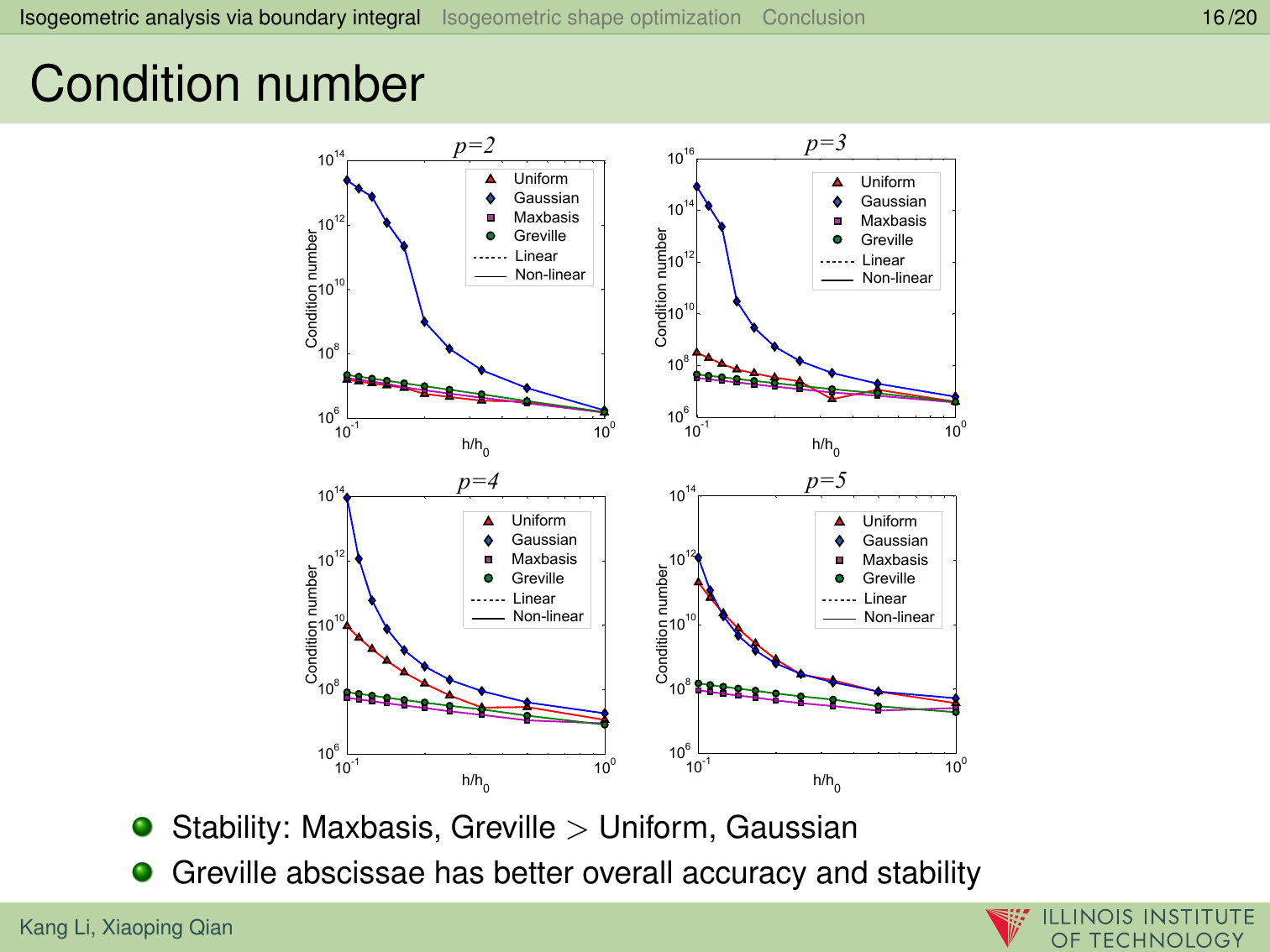
本论文提出了一种基于边界积分的等几何分析和形状优化方法。该方法通过边界积分公式法(Boundary Integral Equation Method 或 BIEM)，使用同一个基函数来表达实体边界和拟合分析物理场，即非均匀有理样条（NURBS）基函数。我们提出将Greville坐标点作为边界配置点，并以线弹性问题进行了h型，p型和k型网格细分实验。实验显示Greville坐标点配置计算结果总体来说收敛性和稳定性都很好；与线性B样条相比，有理B样条形状函数拟合求解空间，分析收敛性并未获得显著改善。为了进行形状优化，我们用NURBS对实体边界参数化，并且提出了一种基于梯度导数的优化方法，并推导出了目标函数和约束函数相对于NURBS控制点位置灵敏度的解析公式。两个工程实例展示了基于边界积分的等几何分析和形状优化方法十分有效，并具备以下优点：1）基于NURBS的边界积分，和传统拉格朗日多项式基函数比，收敛性具有显著优势；2）省去了等几何分析优化中的一大瓶颈：实体内部参数化的过程；3）由于输入几何和输出分析模型使用同一NURBS数据，因为使CAD和分析的结合更加紧密。